Thank you for visiting our site! You landed on this page because you entered a search term similar to this: convert mixed number to decimal.We have an extensive database of resources on convert mixed number to decimal. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter!
| Practice Problems: | Answers: |
Rule 2: To multiply fractions or mixed numbers:1) Convert all mixed numbers to fractions
2) Multiply the numerators together and multiply the denominators together.(In multiplication one can reduce before performing the operation.)
Example:
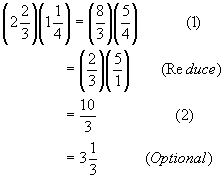
Rule 3: To divide fractions or mixed numbers:1) Convert all mixed numbers to fractions
2) Invert the divisor and change the operation to multiplication
3) Complete the multiplication
Example:
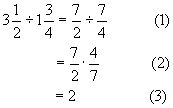
Notation: Whole number exponents tell the number of times touse the base as a factor
Example:
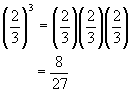
Definition: 
=b if and only if bn = a for some number b
Exampl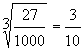e: 
since
| Practice Problems: | Answers: |
 |  |
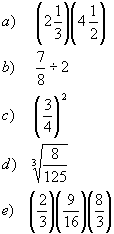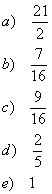2) Fill in trailing zeros
3) Add or subtract as you would whole numbers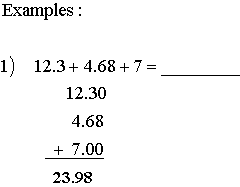
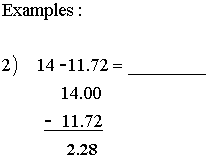
Rule 5: To multiply decimals:1) Multiply as you would whole numbers
2) Count the number of decimal places in each factor
3) Mark off the same number of decimal places in the answer as the sumof the number of decimal places in the factors.
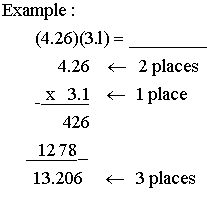
Rule 6: Rule to divide decimals1) Move the decimal behind the last digit in the divisor
2) Move the decimal the same number of decimal places to the right inthe dividend (add zeros if necessary)
3) Divide as with whole numbers, being sure to position digits correctly
4) The decimal in the answer will be directly above the decimal in thedividend
Example:
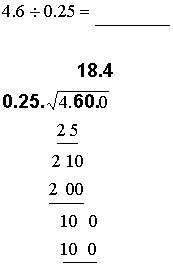
| Practice Problems: a) 2.31 + 7 + 5.6 b) 14.7 - 9.23 c) (28.1)(4.63) d) 269.04 e) (3.1)2
| Answers: a) 14.91 b) 5.47 c) 130.103 d) 5.7 e) 9.61 |
2) Raise to powers and take roots
3) Multiply and divide from left to right
4) Add and subtract from left to right
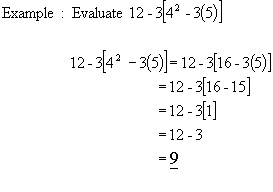Rule 8: To evaluate formulas:1) Replace the letters by their given values
2) Follow the order of operations to evaluate
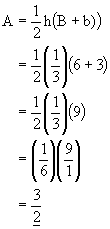
| Practice Problems: Evaluate | Answers: |
| a) 2(3) + 4(6 - 3) b) 4(b + 3C) for b = 2 and C = 5 | a) 18 b) 68 |
Rule 9: To convert:1) Fractions to decimals, divide the numerator by the denominator
2) Decimals to fractions, write the fraction as the decimal is readand reduce
3) Fractions or decimals to percents, multiply by 100%
4) Percents to fractions or decimals, divide by 100%
Examples:
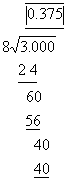2) Convert 0.28 to a fraction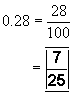
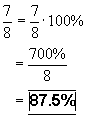4) Convert 26.8% to a decimal
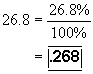5) What is 56% of 320?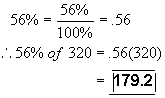
| Practice Problems: Convert as indicated | Answers: |
a) 0.173 to a fraction 
c) 4.3% to a decimal
| 
c) 0.043 d) 0.15 e) 5 |
APPLICATION PROBLEMS
1. A farmer harvested 48,280 pounds of potatoes from onefield and 23,720
pounds from another. The potatoeswere packed in boxes with 24 pounds
per box. How many boxes were neededto pack the potatoes?
2. Bob bought 10 1/3 pounds of hamburger. He used2 pounds to make spaghetti.
How many 1/3-pound burgers canbe made from the remaining hamburger?
3. Three pieces of board, each 2 3/4 feet long, are cutfrom a 10-foot board. How
long is the remaining piece ofboard?
4. Long distance phone calls cost $.45 for the first threeminutes and $.12 for each
additional minute. Find the costof a 15-minute call.
5. John can afford to spend 15% of his monthly pay for rent. If he makes $1300 a
month, how much can he afford to payfor rent?
6. A recent survey indicated that thirty-five percent ofthe students at RCC are
taking math. If 520 students aretaking math, how many students are enrolled
at RCC?
7. A wallpaper hanger charges $255 for labor and materialsfor a particular job.
The cost of materials represents 25%of the total cost. Find out how much the
wallpaper hanger receives for her labor.
8. BB&T wants to know what percent of its customersare late with their loan
payments. A check of 8500 outstandingloans showed that 2550 customers
were late with their payments last month. What percent of BB&Ts customers
were late with their payments last month?
9. In a class of 300 students, 10% received As, 20% received Bs, 20%received
Ds, and 10% received Fs. Howmany students received Cs?
Answers
1. 3000 boxes
2. 25 burgers
3. 1 ¾ feet
4. $1.89
5. $195
6. about 1486 students
7. $191.25
8. 30%
9. 120 students
Part II
Rule 10: To add rational numbers:Case 1 (Signs Alike)
Determine the sum of their absolute values and keep the sign.
Case 2 (Signs Different)
Determine the difference of their absolute values and take the signof the number having the larger absolute value.
Examples:
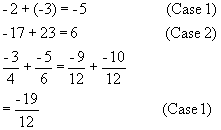
Rule 11: Let a and b be rational numbers:a - b = a + (-b)
Examples:
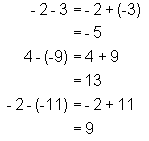Rule 12: To multiply rational numbers, multiply their absolute values.If the numbers have like signs, the answer will be positive. If the numbershave unlike signs, the answer will be negative.Examples:
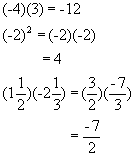
The sign rule for division is similar to the rule for multiplication.
Examples:
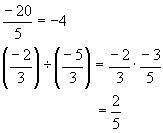
One must not forget the rule for the order of operations:
Example:
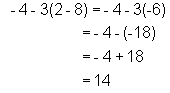
| Practice Problems: | Answers: |
| a) -2 - 3 | a) -5 |
| b) (-4)(5)(-3) | b) 60 |
| c) -6 + 10 | c) 4 |
d) 12  (-2)2 | d) 3 |
| e) -8(-3) - 6(4) | e) 0 |
Rule 13: To combine like terms, keep the common literal partand add the numerical coefficients.Examples:
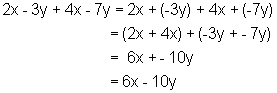
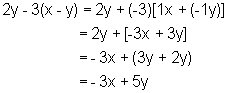
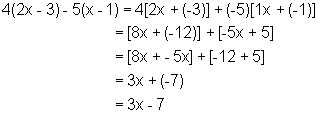
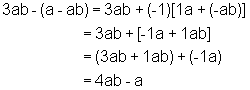
| Practice Problems: | Answers: |
| a) 3a - 4b + a b | a) 4a - 5b |
| b) (x - 3y) - (x + y) | b) -4y |
| c) 3a - 4(2a - 3b) | c) -5a + 12b |
2) Combine like terms
3) Divide both sides by the coefficient of the variable
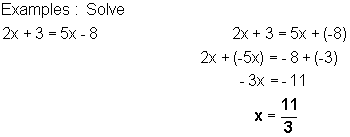
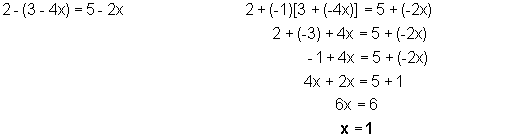
| Practice Problems: | Answers: | |
| Solve for x | ||
| a) 5x - 3 = 2x + 7 |  | |
| b) 4 -(x - l) = -2x + 6 | b) x = 1 | |
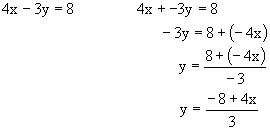Solve for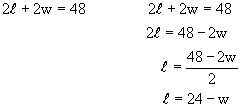 
| Practice Problems: | Answers: | |
| Solve for x | ||
| a) 3x - 4y = 6 |  | |
| b) 2 - 3x = 7a - 1 |  | |
Rule 15: To graph linear equations having two variables:1) Solve for y
2) Make a table of values
3) Plot the points
4) Draw the line
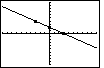
Example: Graph 2x + 3y = 6
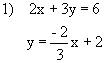
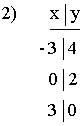
3)
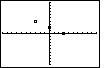4)
Practice Problem:
Graph 2x + y = 1 Answer: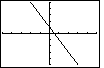 
Part III
Definition: Let x be a rational number and let a and b be naturalnumbers1) 
(xused as a factor a times)
2) 
3) 
4) 
Examples:
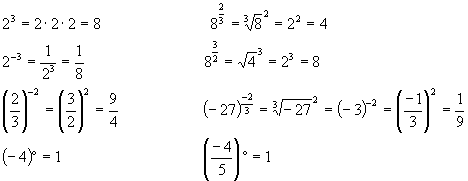
| Practice Problems: | Answers: |
 |  |
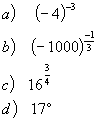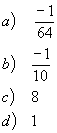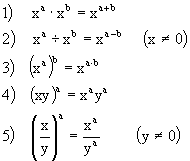Examples: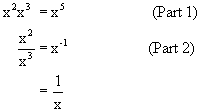
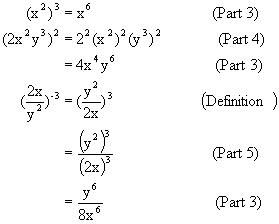
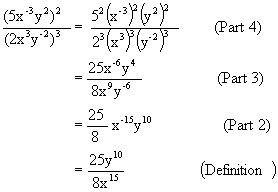
| Practice Problems: | Answers: |
| a) (2x-3y)2(3xy)3 | a)  |
b) 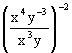 | b)  |
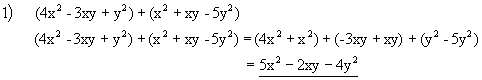
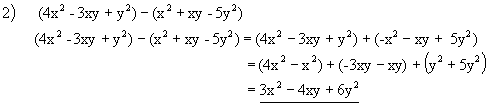
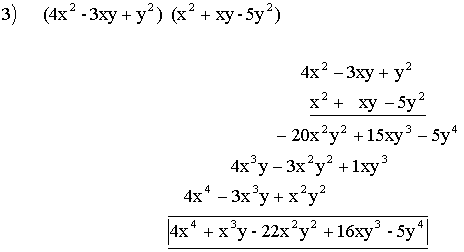
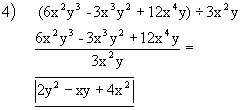
| Practice Problems: Perform the operation.
| Answers: |
 |  |
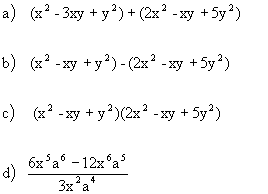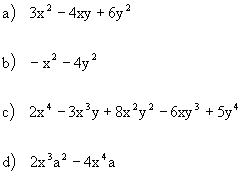Rule 17: To factor polynomials:1) Factor out the greatest common factor.
2) If you have two terms, use a formula.a2 - b2 = (a - b)(a + b)
a3 - b3 = (a - b)(a2 + ab + b2)
a3 + b3 = (a + b)(a2 - ab + b2)3) If you have three terms, use trial and error.
4) If you have more than three terms, try to group to create one ofthe above conditions.
5) Be sure to repeat above steps until all factors are prime.
Examples:
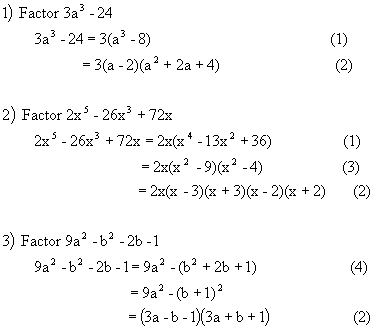
| Practice Problems: Completely factor. | Answers: |
 |  |
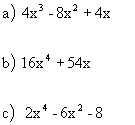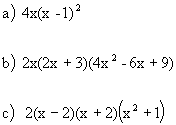The procedures for performing operations on algebraic fractions aresimilar to those for common fractions.
Examples:
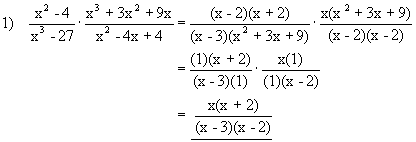
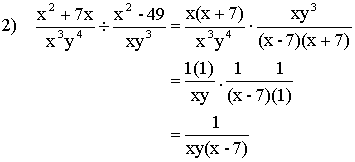
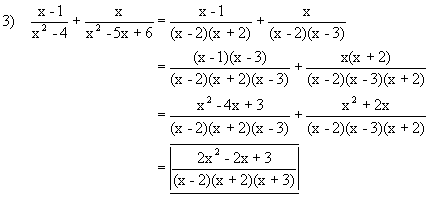
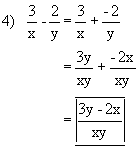
| Practice Problems: | Answers: |
 |  |
Properties of Radicals: Let aand b denote real numbers
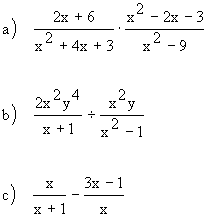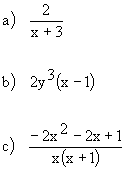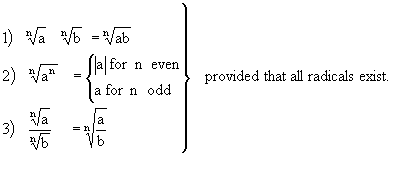Rule 18: To write radical expressions in simplest terms:1) Rationalize denominators.2) Reduce radicals.
3) Reduce indices.
Examples: (Assume that all variables represent positive real numbers.)
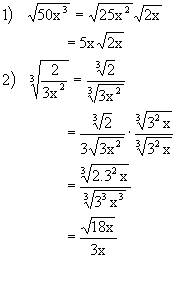
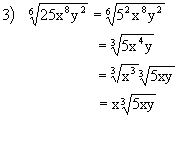
| Practice Problems: Simplify. | Answers: |
 |  |
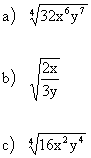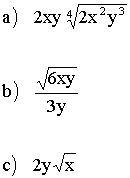