Quadratic Functions
Example 2 Find the maximum area inclosed by 1000
yards of fence for six
rectangular corrals in the following configuration.
In this example there are four vertical fence lines and
three horizontal
fence lines. So we have the relation
4x + 3y = 1000
If we solve for y we have
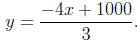Then the area would be given by
the function
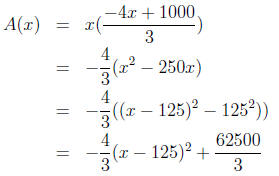
Thus we see that the length of the vertical sides are 125
yards and the
maximum area would be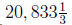 
square yards . The
length of the horizontal
sides would then be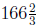 
yards.
§5.6 The Quadratic Formula
If we consider the general quadratic function f(x) = ax2
+ bx + c and
complete the square we compute the following
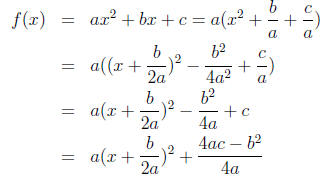
So the vertex is
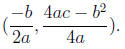
Now if we set f(x) = 0 and solve for x we compute
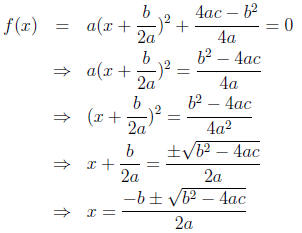
The last equation is the Quadratic Formula.
Example 1 Use the quadratic formula to find the
zeros of f(x) = 2x2−3x+1.
Here we note that a = 2, b = −3 and c = 1, so we have
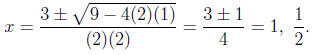
Example 2 Use the quadratic formula to find the
zeros of f(x) = 2x2 + 1.
Here we note that a = 2, b = 0 and c = 1, so we have
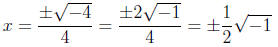
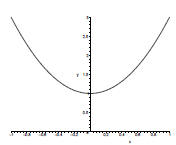
Since there is no real number when squared will be
negative, we conclude
that this function has no real zeros. The graph of this function shows
clearly demonstrates that fact as well.
§5.7 Complex Numbers
Just because the function f(x) = 2x2 + 1. doesn’t have
any roots in
the Real numbers, does not mean it doesn’t have roots in some other set of
numbers.
Consider the following sequence of functions and their roots.
Lets begin by assuming that the only numbers that we know
are the
Natural or Counting numbers, {1, 2, 3, · · · }
Consider the function f(x) = x − 1, it’s zero is 1 which
is a counting
number.
Now consider the function f(x) = x + 1, it’s zero is −1,
which is not a
counting number. But if all we have are the counting numbers then we have
no root. So we enlarge the counting numbers to include the negative counting
numbers and zero, which we call the integers, {· · · ,−2,−1, 0, 1, 2, · · · }.
And
now we can have zeros to functions like f (x) = x + c where c is a counting
number.
Now consider the function f(x) = 2x − 1, it’s zero is 1/2
which is not an
integer! So again if all we have are the integers we do not have a root to this
function. So again we enlarge the integers to include all possible fractions ,
which we call the rational numbers ,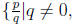 
and p, q
are integers with no
common factors }. So again we can have zeros to functions like f(x) = ax+b
where a and b are integers.
OK, now consider the function f(x) = x2 − 2. It has two
zeros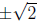 
and
neither one is rational! So we must enlarge our set of numbers to include the
real numbers to solve equations such as this.
Let us now consider one more function f(x) = x2 + 1. If
it has zeros,
they would have to be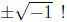 
And neither one of
these numbers could
possibly be real. So we must again enlarge our set of numbers to include
these possible roots.
Definition We say
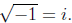We do this mostly for convenience, so we
don’t
have to write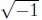 
over and over again.
Definition We say that a complex number is a number
of the form a + bi
where a and b are real numbers. We call a the real part of the complex number
and b is the imaginary part of the real number. So a complex number is the
formal sum of a real number and the product of a real number times
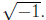
If the real numbers are represented by the real number
line, then the
complex numbers (where b ≠ 0) cannot be on the real number line. So where
are they?
We note that i is not real, so we place it one unit above
0 on the x-axis,
and we draw a second copy of the real numbers perpendicular through the
origin and through the point labelled i, and we label the corresponding points
on the vertical axis with multiples of i .
Now every point in the plane formed by these two axis
represents a com-
plex number, where the real part is indicated by its horizontal distance from
the vertical axis and the imaginary part is indicated by its vertical distance
from the horizontal axis. For example the points 2 + 2i, −1 + i, and 2 − 3i
are indicated on the graph below.
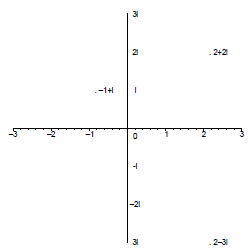
§5.8 Complex Arithmetic
The general strategy of arithmetic with complex numbers is
to treat the
complex numbers as binomials, and then do binomial arithmetic remember-
ing that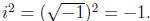 
Let a + bi and c + di be complex numbers, e.g. 2 + 3i, and 1 − 4i
(a + bi) + (c + di) = (a + c) + (b + d)i,
e.g.
(2 + 3i) + (1 − 4i) = 3 − i.
(a + bi) − (c + di) = (a − c) + (b − d)i,
e.g.
(2 + 3i) − (1 − 4i) = 1 + 7i.
MULTIPLICATION
(a + bi) · (c + di) = a · c + a · di + c · bi + b · d · i2
ac + bd(−1) + (ad + bc)i = (ac − bd) + (ad + bc)i
e.g.
(2 + 3i) · (1 − 4i) = 2 · 1 − 3 · (−4) + (3 − 8)i = 14 − 5i.
DIVISION
Division is a little trickier, but still not too bad.
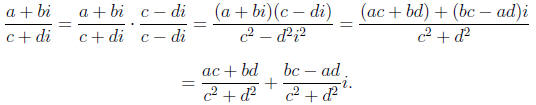
e.g.
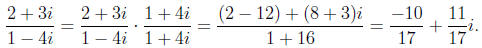
Now we look at the quadratic formula
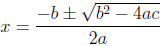and recognize
that when b2 − 4ac is positive we will have two real roots, but if b2 − 4ac is
negative we will have two non-real roots of the form A+Bi and A−Bi, where
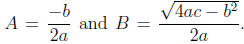The remaining case is where b2 − 4ac = 0,
in this case there is one root,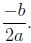 
The expression b2 − 4ac is called the
discriminant since it discriminates between the natures of the roots of the
quadratic function.
| Prev | Next |