Inverse Functions

I. Inverse Functions

If we form the composition of two functions , we should get
the identity function h (x) = x. So to speak, inverse
functions “undo” each other. Also note that if a function is
given as a set of ordered pairs , its inverse has all the x-coordinates
interchanged with their corresponding y-
coordinates .

Ex: f (x) = x + 2 and g (x) = x – 2 are inverses because
f (g (x)) = f (x - 2) = (x - 2) + 2 = x, and
g (f (x)) = g (x + 2) = (x + 2) – 2 = x.

The functions f and g are inverses of each other iff:
1. f (g (x)) = x for every x in the domain of g, and
2. g (f (x)) = x for every x in the domain of f.
In this case we write g (x) as f ^-1(x)

This is NOT a negative exponent it is just the notation

II. The Graph of an Inverse Function
If we interchanged the x’ s and y’ s for every point on the
graph of a function , the graph would be reflected about
the line y = x.

Ex: f (x) = x – 1 and f ^-1(x) = x + 1

III. One-to-One Functions

Draw the graph of y = x². Reflect it about the line y = x.
Is this inverse a function.
When is the inverse of a function a function?

This brings us to the Horizontal Line Test :

• If every horizontal line meets the graph of a function
in at most one point, then the inverse of this function
will be a function.

• If no horizontal line intersects the graph of a function
in more than one point, no x- value is matched with
more than one y- value .

This brings us to the definition of a one-to-one function:
• A function f is one-to-one if each value of the
dependent variable corresponds to exactly one value
of the independent variable .

A function has an inverse iff the function is one-to-one.

Ex: Which of the following functions has an inverse
function?

(a) f (x) = |x|

(b) g (x) = x³

IV. Finding Inverse Functions Algebraically

Steps for finding the inverse of a function:
If the function is one-to-one
1. Replace f (x) with y.
2. Interchange the roles of x and y.
3. Solve this new equation for y .
4. Replace y by f ^-1(x).

Ex: Find the inverse of each of the following functions.


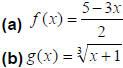
(c) h (x) = x ²  for x ≥ 0