MATRIX OPERATIONS
Summary of article :
What is an operation?
Addition of two matrices .
Multiplication of a Matrix by a scalar.
Subtraction of two matrices : two ways to do it.
Combinations of Addition, Subtraction, Scalar Multiplication.
Matrix Multiplication
An operation is a way that we combine two elements.
The basic operations are:
Addition (+)
Subtraction (-)
Multiplication ( * )
Division ( ÷ )
Here are some examples of combining elements and the operations used :
Combining elements that are rational numbers ( fractions ) using the operation of
addition.
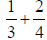
Combining elements that are second degree binomials using the operation of
multiplication.
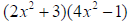
Combining elements that are integers using the operation of division.
−35 ÷ 7
This FAQ will review the definitions of addition, scalar multiplication,
subtraction, and
the multiplication of matrices. Division is undefined for matrices, but there is
a separate
related concept, Inverse Matrices, that is similar to division and is found
among the other
FAQ topics listed on the Online Math Center .
ADDITION of TWO MATRICES
To add two matrices, their orders (the number of rows and columns in both
matrices)
must be the same.
Add the corresponding row-column elements from each Matrix to produce a new
element
in the same row-column location.
Example 1: Both matrices are order 2 x 2
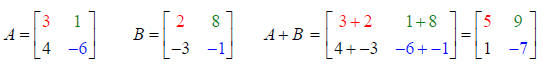
Example 2: Both matrices are order 3 x 5
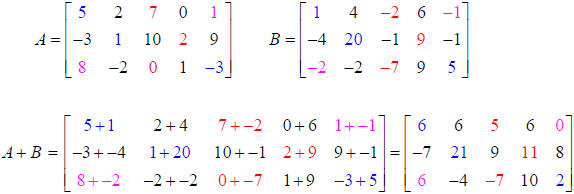
MULTIPLICATION of a MATRIX by a scalar
A scalar is simply a number . To multiply a Matrix by a scalar, distribute the
scalar to all
elements in the Matrix and multiply.
Example 1: Multiply Matrix A by the scalar 3:
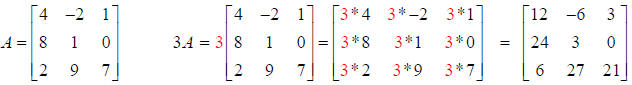
Example 2: Multiply Matrix B by the scalar
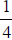 :
:
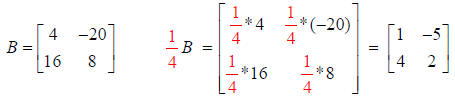
SUBTRACTION of TWO MATRICES
To subtract two matrices, their orders (the number of rows and columns in both
matrices)
must be the same.
The easy way…
To subtract Matrix A and B, simply subtract corresponding row-column elements.
Don’t forget to change signs of elements in Matrix B
Example 1: Subtract Matrix B from Matrix A. Both are order 2 x 2.
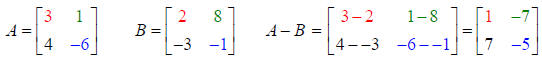
Example 2: Subtract Matrix B from Matrix A. Both are order 1 x 4.
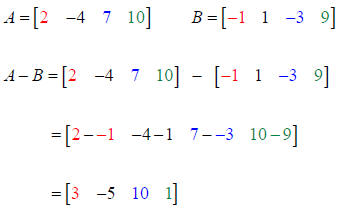
Example 3: Subtract D from C
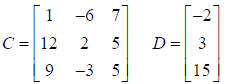
Matrix C is a 3 x 3 order Matrix. Matrix D is a 3 x 1
order Matrix.
Since the order of the two matrices is different , they can NOT be subtracted.
Now the mathematics behind the scenes…
The negative sign in front of the second Matrix is actually the scalar “ −1”.
Distribute the scalar “ −1” to all elements in the second Matrix.
Add the corresponding row-column elements from each Matrix to produce a new
element
in the same row-column location.
Example: Subtract B from A
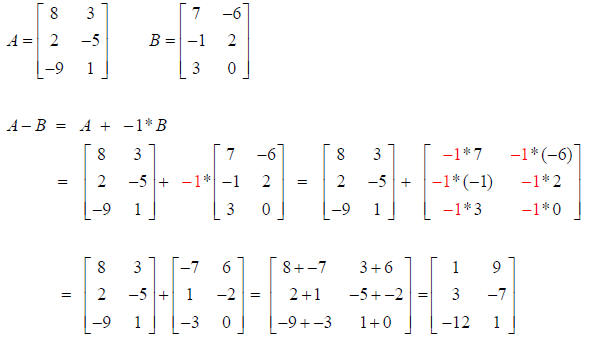
COMBINATIONS of ADDITION, SUBTRACTION, and Scalar
MULTIPLICATION.
The order of operations requires multiplication be done before addition or
subtraction, so
first multiply the elements inside a Matrix by the scalar in front of it. Add
and/or subtract
afterwards.
Example:
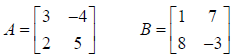
Find 3A− 5B
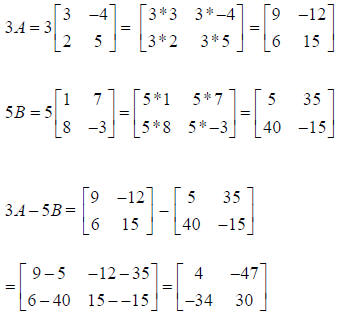
MULTIPLICATION of TWO MATRICES
Two matrices A and B can be multiplied if the number of columns in A is
the same as
the number of rows in B. The new Matrix will have the same number of rows
as A and
the same number of columns as B.
Example, find A* B
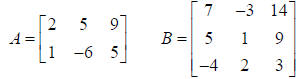
Matrix A is 2 x 3 (2 rows, 3 columns).
Matrix B is a 3 x 3 (3 rows, 3 columns) Matrix.
The columns in A equal the rows in B, so we can multiply A*B producing a 2 x 3
Matrix.
However, the columns in B do not equal the rows in A, so we can not multiply
B*A.
Steps in multiplying two matrices
1. Determine if the two matrices can be multiplied, i.e. the number of columns
in A
equals the number of rows in B.
If the order of A is (m x n) and the order of B is (n x p), the new Matrix will
be of
order (m x p).
2. Set up the new, blank (m x p) Matrix.
3. Pick a row-column location of an element in the new Matrix, e.g. the element
in
row 1 column 1 of the new Matrix.
4. Multiply the first element from the identified row in A by the first element
in the
identified column of B. Multiply the second element from the identified row of A
by the second element in the identified column of B. Continue across the row of
A
and down the column of B. Then add all of the results. Place the answer in the
new Matrix at the row-column location identified.
5. Continue until all row-column locations of the new Matrix are filled.
Example: 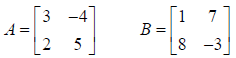
Matrix A has 2 rows and 2 columns; Matrix B has 2 rows and
2 columns. The number of
columns in A equals the number of rows in B, so the two matrices can be
multiplied.
The (2 x 2) times (2 x 2) will produce a new (2 x 2) Matrix. Set up the new,
blank 2 x 2
Matrix.
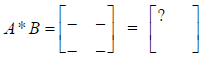
The question mark has been placed in the first row, first
column location of the new
Matrix. So multiply the first element in row 1 of Matrix A by the first element
in column
1 of Matrix B. Then multiply the second element in row 1 of Matrix A by the
second
element in column 1 of Matrix B.
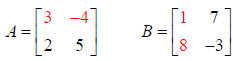
Multplying row 1 of A by column 1 of B:
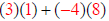
We have gone across row 1 in Matrix A and down column 1 in
Matrix B, so we can add
the results and place the answer in row 1-column 1 of the new Matrix
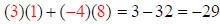 New Matrix: row 1,
column 1:
New Matrix: row 1,
column 1: 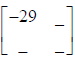
Now let’s find the element for row 1, column 2:
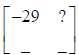
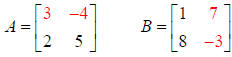
Multplying row 1 of A by column 2 of B:
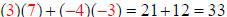
So row 1, column 2 of the new Matrix is the element 33:
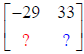
For row 2, column 1 multiply row 2 of Matrix A and
column 1 of Matrix B.
For row 2, column 2 multiply row 2 of Matrix A and column 2 of matrix B:
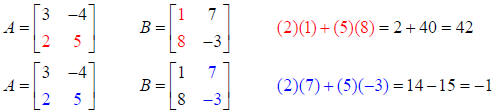
Hence:
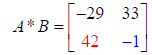
Example: Find A * B 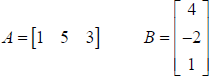
A is order (1 x 3) and B is order (3 x 1), so the new
matrix will be order (1 x 1): [?]
There is only one element in the new matrix: the row 1, column 1 element.
Multiply row 1 elements of Matrix A by column 1 elements of Matrix B and add the
result.
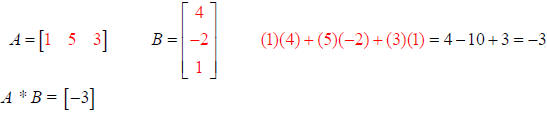
Example: Find A * B 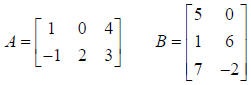
A is order (2 x 3) and B is order (3 x 2), so the new matrix will be order (2 x 2):
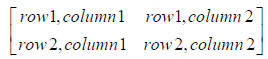
Row 1, Column 1: (1)(5) + (0)(1) + (4)(7) = 5 + 0 + 28 =
33
Row 1, Column 2: (1)(0) + (0)(6) + (4)(−2) = 0 + 0 −8 = −8
Row 2, Column 1: (−1)(5) + (2)(1) + (3)(7) = −5 + 2 + 21 =18
Row 2, Column 2: (−1)(0) + (2)(6) + (3)(−2) = 0 +12 − 6 = 6
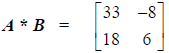
| Prev | Next |