Maximum and Minimum Values
A quadratic function , f, is a function that can be
put in the form,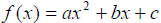 
where a, b, and care real numbers and a is not equal to zero.
A quadratic function, f, can be expressed in the form,
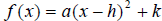called the standard
form by the method of completing the square.
The axis of symmetry is the vertical line x = h. It divides the graph in half .
Properties of a Quadratic Function and Its Graph
Given a quadratic function in the form,
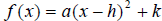with a not equal to zero .
1. The graph of f is a parabola .
2. The vertex is (h, k).
3. If a> 0, the parabola opens upward and it has a minimum value which is k.
4. If a< 0 the parabola opens downward and it has a maximum value which is k.
5. Every parabola will have a minimum or maximum value, but not both.
6. The axis of symmetry is the vertical line x = h.
Example 1: For the given quadratic function, determine if
it has a maximum or minimum value
and then find the vertex.
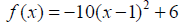
Example 2: For the given quadratic function, determine if
it has a maximum or minimum value
and then find the vertex.
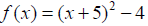
Example 3: Determine whether the following quadratic
function has a maximum or minimum
value. Then write the quadratic function in standard form and find the maximum
or minimum
value.
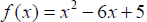
Example 4: Determine whether the following quadratic
function has a maximum or minimum
value. Then write the quadratic function in standard form and find the maximum
or minimum
value.
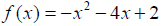
Finding the Vertex of a Quadratic Function
Given a quadratic function in the form,
the vertex is
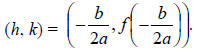
Example 5: For the following quadratic function, find the vertex.
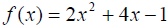
Example 6: For the following quadratic function, find the
coordinates of the maximum or
minimum point.
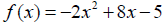
Graphing Quadratic Functions with Equations in Standard Form
1. Determine whether the parabola opens upward or
downward.
2. Determine the vertex.
3. Find any x- intercept by replacing f(x) with 0 and then solving for x .
4. Find the y- intercept by replacing x with 0.
5. Plot the intercept (s) and vertex, sketch the graph and draw the axis of
symmetry.
Example 7: Sketch the graph of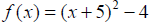 
Example 8: Sketch the graph of
.
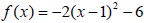Example 9: Find a quadratic function satisfying the given
conditions.
Vertex: (-3, -1); passes through (2, -101)
| Prev | Next |