Dividing Fractions
Class Activity 0C: "How Many in One Group?" Frac-
tion Division Problems
Class Activity 0D: Are These Division Problems?
Exercises for Section 0.1 on Dividing Fractions
1. Write a "how many groups?" story problem for
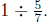 Use the story
Use the story
problem and a diagram to help you solve the problem .
2. Write a "how many in one group?" story problem for
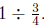 Use the
Use the
situation of the story problem to help you explain why the answer is
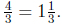
3. Annie wants to solve the division problem 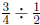 by using the following
by using the following
story problem:
I need ![]() cup of
chocolate chips to make a batch of cookies.
cup of
chocolate chips to make a batch of cookies.
How many batches of cookies can I make with
![]() of a cup of
of a cup of
chocolate chips?
Annie draws a diagram like the one in Figure 3. Explain why it would
be easy for Annie to misinterpret her diagram as showing that
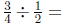
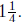 How should Annie interpret her diagram so as
to conclude that
How should Annie interpret her diagram so as
to conclude that
![]()
4. Which of the following are solved by the division problem
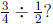 For
For
those that are, which interpretation of division is used? For those that
are not, determine how to solve the problem, if it can be solved.
(a) ![]() of a bag of jelly
worms make
of a bag of jelly
worms make ![]() a cup. How
many cups of jelly
a cup. How
many cups of jelly
worms are in one bag?
|
1/2 cup makes one batch |
 |
1/4 cup left |
Figure 3: How Batches of Cookies Can We Make With
![]() of a Cup of Chocolate
of a Cup of Chocolate
Chips if 1 Batch Requires
![]() Cup of Chocolate
Chips?
Cup of Chocolate
Chips?
(b)
![]() of a bag of jelly
worms make
of a bag of jelly
worms make
![]() a cup. How many bags
of jelly
a cup. How many bags
of jelly
worms does it take to make one cup?
(c) You have ![]() of a bag
of jelly worms and a recipe that calls for
of a bag
of jelly worms and a recipe that calls for
![]() of
of
a cup of jelly worms. How many batches of your recipe can you
make?
(d) You have ![]() of a cup
of jelly worms and a recipe that calls for
of a cup
of jelly worms and a recipe that calls for
![]() of
of
a cup of jelly worms. How many batches of your recipe can you
make?
(e) If ![]() of a pound of
candy costs
of a pound of
candy costs ![]() of a
dollar, then how many pounds
of a
dollar, then how many pounds
of candy should you be able to buy for 1 dollar?
(f) If you have ![]() of a
pound of candy and you divide the candy in
of a
pound of candy and you divide the candy in
![]() ,
,
then how much candy will you have in each portion?
(g) If ![]() of a pound of
candy costs $1, then how many dollars should
of a pound of
candy costs $1, then how many dollars should
you expect to pay for ![]() of a pound of candy?
of a pound of candy?
5. Frank, John, and David earned $14 together. They want to divide it
equally, except that David should only get a half share, since he did half
as much work as either Frank or John did (and Frank and John worked
equal amounts). Write a division problem to find out how much Frank
should get. Which interpretation of division does this story problem
use?
6. Bill leaves a tip of $4.50 for a meal. If the tip is 15% of the cost of
the meal, then how much did the meal cost? Write a division problem
to solve this. Which interpretation of division does this story problem
use?
7. Compare the arithmetic needed to solve the following
problems.
(a) What fraction of a ![]() cup measure is filled when we pour in
cup measure is filled when we pour in 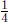 cup
cup
of water?
(b) What is one quarter of
![]() cup?
cup?
(c) How much more is ![]() cup than
cup than 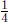 cup?
cup?
(d) If 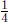 cup of water fills
cup of water fills
![]() of a plastic
container, then how much
of a plastic
container, then how much
water will the full container hold?
8. Use the meanings of multiplication and division to solve the following
problems.
(a) Suppose you drive 4500 miles every half year in your car. At the
end of 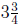 years, how many miles will you have
driven?
years, how many miles will you have
driven?
(b) Mo used 128 ounces of liquid laundry detergent in
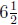 weeks. If
weeks. If
Mo continues to use laundry detergent at this rate, how much will
he use in a year?
(c) Suppose you have a 32 ounce bottle of weed killer concentrate.
The directions say to mix two and a half ounces of weed killer
concentrate with enough water to make a gallon. How many gallons
of weed killer will you be able to make from this bottle?
9. The line segment below is
![]() of a unit long. Show
a line segment that
of a unit long. Show
a line segment that
is 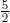 of a unit long. Explain how this problem
is related to fraction
of a unit long. Explain how this problem
is related to fraction
division.
![]() unit
unit
Answers To Exercises For Section 0.1 on Dividing Frac-
tions
1. A simple "how many groups?" story problem for
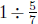 is "how many
is "how many
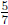
of a cup of water are in 1 cup of water?" Figure 4 shows 1 cup of water
and shows 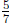 of a cup of water shaded. The
shaded portion is divided
of a cup of water shaded. The
shaded portion is divided
into 5 equal parts and the full cup is 7 of those parts. So the full cup
is 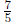 of the shaded part. Thus there are
of the shaded part. Thus there are
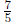 of
of 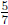 of a
cup of water in 1
of a
cup of water in 1
cup of water, so 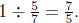
| 1 cup | 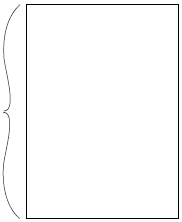 |
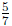 of a cup
of a cup |
 |
of the shaded portion |
Figure 4: Showing Why 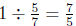 by Considering How Many
by Considering How Many ![]() of a Cup of
of a Cup of
Water are in 1 Cup of Water
2. A "how many in one group?" story problem for
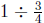 is "if 1 ton of
is "if 1 ton of
dirt fills a truck ![]() full, then how many tons of dirt will be needed to
full, then how many tons of dirt will be needed to
fill the truck completely full?". We can see that this is a "how many
in one group?" type of problem because the 1 ton of dirt fills
![]() of a
of a
group (the truck) and we want to know the amount of dirt in 1 whole
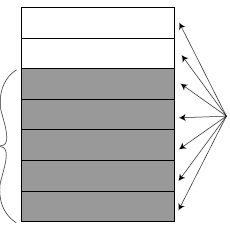
group. Figure 5 shows a truck bed divided into 4 equal parts with 3
of those parts filled with dirt. Since the 3 parts are filled with 1 ton
of dirt, each of the 3 parts must contain
![]() of a ton of dirt. To
ll the
of a ton of dirt. To
ll the
truck completely, 4 parts, each containing
![]() of a ton of dirt are
needed.
of a ton of dirt are
needed.
Therefore the truck takes 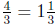 tons of dirt to
fill it completely, and
tons of dirt to
fill it completely, and
so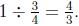
|
the 1 ton of dirt is divided equally among 3 parts |
 truck bed |
4 parts are needed to fill the truck; each part is 1/3 of a ton, so 4/3 tons of dirt are needed to fill the truck |
Figure 5: Showing Why 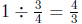 by Considering How Many Tons of Dirt
by Considering How Many Tons of Dirt
it Takes to Fill a Truck if 1 Ton Fills it ![]() Full
Full
3. Annie's diagram shows that she can make 1 full batch of cookies from
her
![]() of a cup of chocolate
chips and that
of a cup of chocolate
chips and that ![]() cup of
chocolate chips will
cup of
chocolate chips will
be left over. Because ![]() cups of chocolate chips are left over, it would
cups of chocolate chips are left over, it would
be easy for Annie to misinterpret her picture as showing
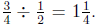
But the answer to the problem is supposed to be the number of batches
Annie can make. In terms of batches , the remaining
![]() cup of chocolate
cup of chocolate
chips makes ![]() of a batch
of cookies. We can see this because 2 quarter-cup
of a batch
of cookies. We can see this because 2 quarter-cup
sections make a full batch, so each quarter-cup section makes
![]() of
of
a batch of cookies. So by interpreting the remaining
![]() cup of chocolate
cup of chocolate
chips in terms of batches , we see that Annie can make
![]() batches of
batches of
chocolate chips, thereby showing that 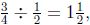 not
not
![]()
4. (a) This problem can be rephrased as "if
![]() of a cup of jelly
worms
of a cup of jelly
worms
fill ![]() of a bag, then
how many cups fill a whole bag?", therefore
of a bag, then
how many cups fill a whole bag?", therefore
this is a "how many in one group?" division problem illustrating
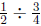 , not
, not 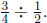 Since
Since 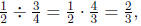 there are
there are
![]() of a cup of
of a cup of
jelly worms in a whole bag.
(b) This problem is solved by 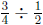 ,according to
the "how many in
,according to
the "how many in
each group?" interpretation. A group is a cup and each object is
a bag of jelly worms.
(c) This problem can't be solved because you don't know how many
cups of jelly worms are in
![]() of a bag.
of a bag.
(d) This problem is solved by 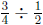 , according to
the "how many
, according to
the "how many
groups?" interpretation. Each group consists of
![]() of a cup of jelly
of a cup of jelly
worms.
(e) This problem is solved by 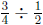 , according to
the "how many in
, according to
the "how many in
one group?" interpretation. This is because you can think of the
problem as saying that ![]() of a pound of candy fills
of a pound of candy fills ![]() of a group
of a group
and you want to know how many pounds fills 1 whole group.
(f) This problem is solved by 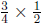 , not
, not
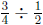 . It is dividing in half,
. It is dividing in half,
not dividing by ![]() .
.
(g) This problem is solved by 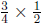 , according to
the "how many
, according to
the "how many
groups?" interpretation because you want to know how many
![]()
pounds are in ![]() of a
pound. Each group consists of
of a
pound. Each group consists of
![]() of a pound
of a pound
of candy.
5. If we consider Frank and John as each representing one group, and
David as representing half of a group, then the $14 should be dis-
tributed equally among 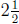 groups. Therefore, this is a "how many in
groups. Therefore, this is a "how many in
one group" division problem. Each group should get
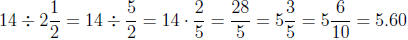
dollars. Therefore Frank and John should each get $5.60
and David
should get half of that, which is $2.80.
6. According to the "how many in one group?" interpretation, the problem
is solved by $4.50 ÷ 0.15 because $4.50 fills 0.15 of a group and we
want to know how much is in 1 whole group. So the meal cost
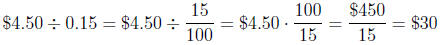
7. Each problem, except for the first and last, requires
different arithmetic
to solve it.
(a) This is asking: ![]() equals what times
equals what times ![]() ? We
solve this by calculating
? We
solve this by calculating
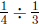 , which is
, which is
![]() . We can also think
of this as a division problem
. We can also think
of this as a division problem
with the "how many groups?" interpretation because we want to
know how many ![]() of a
cup are in
of a
cup are in ![]() of a cup.
According to the
of a cup.
According to the
meaning of division, this is 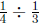 .
.
(b) This is asking: what is
![]() of
of
![]() ? We solve this by
calculating
? We solve this by
calculating
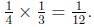
(c) This is asking: what is 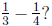 The answer is
The answer is
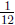 which happens to
which happens to
be the same answer as in part (b), but the arithmetic to solve it
is different.
(d) Since ![]() cup of water
fills
cup of water
fills ![]() of a plastic
container, the full container
of a plastic
container, the full container
will hold 3 times as much water, or 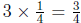 of a
cup. We can
of a
cup. We can
also think of this as a division problem with the "how many in one
group?" interpretation. ![]() cup of water is put into
cup of water is put into
![]() of a group.
of a group.
We want to know how much is in one group. According to the
meaning of division it's 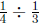 , which again is
equal to
, which again is
equal to ![]() .
.
8. (a) The number of ![]() years in
years in 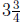 years is
years is
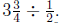 There will be that
There will be that
many groups of 4500 miles driven. So after 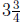 years you will have
years you will have
driven
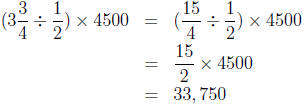
miles.
(b) Since one year is 52 weeks there are 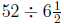 groups of
groups of 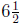 weeks
weeks
in a year. Mo will use 128 ounces for each of those groups, so Mo
will use
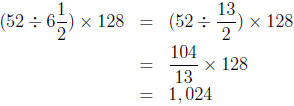
ounces of detergent in a year.
(c) There are 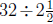 groups of
groups of
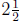 ounces in 32 ounces. Each of those
ounces in 32 ounces. Each of those
groups makes 1 gallon. So the bottle makes 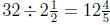 gallons
gallons
of weed killer.
9. One way to solve the problem is to determine how many
![]() units are in
units are in
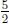
units. This will tell us how many of the
![]() unit long segments to
lay end
unit long segments to
lay end
to end in order to get the 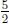 unit long
segment. Since
unit long
segment. Since 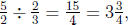
there are 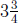 segments of length
segments of length
![]() units in a segment of
length
units in a segment of
length 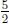 units.
units.
So you need to form a line segment that is 3 times as long as the one
pictured, plus another ![]() as long:
as long:

| Prev | Next |