Basic_Algebra_Course2
Departmental Course Syllabus
Department: Mathematics /Computer Science Date: 08/22/08
San Antonio College * 1300 San Pedro* San Antonio, TX* 78212-4299
Course Number and Title : Math 0302.103 - Elementary Algebra
Credit Hours: 3
Instructor: Mr. Strottner
Office: NTC 233
Phone Number: 733-2786/2881
Office hours:
Email: pstrottner@mail.accd.edu Web Address: www.accd.edu/sac/math/dept.htm
I. Catalog Description: Content includes factoring techniques, radical
expressions and equations, rational exponents, complex numbers, solving
quadratic equations by various methods, rational expressions and equations, and
related applications.
II. Pre-requisites, co-requisites and other requirements: Math 0301 with a grade of “C” or better, or equivalent. Course placement advisement is available-contact Mathematics/Computer Science Office located at MCCH 221.
III. Text: Elementary and Intermediate Algebra for College Students, 2nd Edition, by Allan R. Angel, Pearson
IV. Instruction will consist of: lecture, homework assignments, group problem solving, classroom discussions, other
V. Course Content: Upon successful completion of this course the student will have demonstrated an understanding of the material contained in the following list of topics:
Chapter 5 Factoring
5.1 Factoring a Monomial from a Polynomial
5.2 Factoring by Grouping
5.3 Factoring Trinomials of the form ax^2+bx+c, a = 1
5.4 Factoring Trinomials of the form ax^2+bx+c, a ≠ 1
5.5 Special Factoring formulas & a General Review of Factoring
5.6 Solving Quadratic Equations using Factoring
5.7 Applications of Quadratic Equations
Chapter 6 Rational Expressions and Equations
6.1 Simplifying Rational Expressions
6.2 Multiplication & Division of Rational Expressions
6.3 Addition and Subtraction of Rational Expressions with a Common Denominator.
Finding the LCD
6.4 Addition and Subtraction of Rational Expressions
6.5 Complex Fractions
6.6 Solving Rational Equations
6.7 Rational Equations: Applications & Problem Solving
Chapter 7 Roots, Radicals, and Complex Numbers
7.1 Roots and Radicals
7.2 Rational Exponents
7.3 Simplifying Radicals
7.4 Adding, Subtracting, and Multiplying Radicals
7.5 Dividing Radicals
7.6 Solving Radical Equations
7.7 Complex Numbers
Chapter 8 Quadratic Equations and Inequalities
8.1 Solving Quadratic Equations by Completing the Square
8.2 Solving Quadratic Equations by the Quadratic Formula
VII. Course requirements and grade computation.
A. College Requirements:
A written, comprehensive final examination, not to exceed two and one-half hours in length, shall be given at the end of each semester for each course at the regularly scheduled time. Any exceptions to these requirements must be approved by the appropriate dean. Other examinations are given at the discretion of the instructor.
A student who must be absent from a final examination should petition that instructor for permission to postpone the examination. A student absent without permission from a final examination is graded “F.” Postponed examinations result in a grade of “I.” The final exam must be taken within 120 calendar days from the end of the semester or the grade automatically becomes an “F.” (San Antonio College Bulletin, Faculty Handbook - January 1995)
B. Departmental Requirement:
A valid student I.D. and current semester registration in a departmental course
is
required to use departmental learning resources (computers, tutoring, videos,
testing). Schedules and additional rules for use are posted periodically.
Additional information is available on my web page. Learning outcomes, performance objectives and measurements and College Policies are included in the class handout shown there. It is in PDF format and can be downloaded if you need a replacement for this copy
C. Instructor Requirements:
(1) Homework: The homework for all material covered in a given class week will be due at the first lecture period following that class week. If you are absent, it is due at the next class that you attend. To be graded, the homework sections must be turned in together. For each section assignment, do every other odd numbered problem in the “Practice the Skills” “Problem Solving”, and “Challenge Problems” exercises. (i.e. 9, 13, 17, etc for Sec 5.1) All work must be shown for credit. If, after completing a section, you are not yet comfortable with the problems, you may complete more odd numbered problems for additional credit. It is very important for you to do the assigned homework. If you are able to understand and do it, you should have no trouble passing the course. You should ensure that it is neat and legible and you may use the homework to study for tests or the final exam. Please do all your work on only one side of the page and circle the answer to each problem.
(2) Tests: Occasional quizzes will be given through the semester. Quiz grades will be included with homework grades. There will be five tests given during the semester. The first four tests will cover Chapters 5, 6, 7, and 8 respectively. The fifth will be the final exam. On each exam, a grade of zero will be given if it is missed without prior notification or there is no bona fide emergency. There will be No make-up tests.
(3) Computation of Course Grade
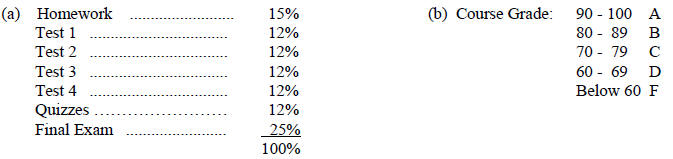
Course Outline
| Class Week | Material Covered | Homework Due |
| 1 Aug 25 | Introduction, Chap 5.1 & 5.2. | |
| 2 Sep 1 | Mon – Holiday, Chap 5.3 & 5.4 | Chap 5.1 & 5.2 |
| 3 Sep 8 | Chap 5.5 & 5.6. | Chap 5.3 & 5.4 |
| 4 Sep 15 | Chap 5.7 & Review. | Chap 5.5 & 5.6 |
| 5 Sep 22 | Test 1, Critique, Chap 6.1. | Chap 5.7 |
| 6 Sep 29 | Chap 6.2 & 6.3. | Chap 6.1 |
| 7 Oct 6 | Chap 6.4 & 6.5. | Chap 6.2 & 6.3 |
| 8 Oct 13 | Chap 6.6 & 6.7 & Review. | Chap 6.4 & 6.5 |
| 9 Oct 20 | Test 2, Critique, Chap 7.1. | Chap 6.6 & 6.7 |
| 10 Oct 27 | Chap 7.2 & 7.3. | Chap 7.1 |
| 11 Nov 3 | Chap 7.4 & 7.5. | Chap 7.2 & 7.3 |
| 12 Nov 10 | Chap 7.6 & 7.7 & Review. | Chap 7.4 & 7.5 |
| 13 Nov 17 | Test 3, Critique, Chap 8.1. | Chap 7.6 & 7.7 |
| 14 Nov 24 | Thurs – Holiday, Chap 8.2 & Review. | Chap 8.1 |
| 15 Dec 1 | Test 4, Critique, Review for Final | Chap 8.2 |
| 16 Dec 11 | Final Exam. 12:15 pm – 2:45 pm |
VI. Learning Outcomes and Performance Objectives with their methods of
measurement as used to determine the students’ mastery of those outcomes.
LEARNING OUTCOMES
A student who passes this course will be able to demonstrate critical thinking with respect to quadratic, rational, and radical expressions and equations. The student will demonstrate the ability to factor selected polynomials, simplify rational and radical expressions, and perform complex number arithmetic. Further, the student will be able to solve selected radical and quadratic equations.
PERFORMANCE OBJECTIVES
The student will identify prime factors and common factors, determine the greatest common factor of two or more terms, and factor the greatest common factor from the terms of a polynomial.
The student will factor polynomials containing four terms by grouping and using common factors, and will factor selected trinomials with integer coefficients of the form ax^2 + bx + c by trial and error or by grouping. The student will also be able to factor the difference of two squares , the sum and difference of two cubes, and selected polynomial expressions that require a combination of the preceding strategies.
The student will solve selected quadratic equations by using factoring techniques and the zero product rule.
The student will simplify a rational expression formed from the addition, subtraction, multiplication or division of rational expressions.
The student will solve selected rational equations, checking the solution set for restrictions, and use these rational equations to model selected applications.
The student will convert a radical expression to exponential form and vice versa.
The student will simplify a radical expression formed from the addition, subtraction, multiplication or division of radical expressions, including rationalizing a denominator .
The student will solve selected radical equations, checking the solution set for restrictions, and use radicals to model selected applications.
The student will identify the real and imaginary components of complex numbers and simplify the sum, difference, product, or quotient of complex numbers.
The student will be able to solve any quadratic equation by using the quadratic formula and/or completing the square method, including quadratics that are prime over the integers.
PERFORMANCE MEASUREMENT
Performance will be measured using a written comprehensive final exam. Additional measures may include but are not limited to exams, quizzes, homework, class participation, collaborative learning, lab activities, project presentations etc. The weight assigned to each measure will be determined by the individual instructor.
VIII. College Policies:
A. San Antonio College does not discriminate on the basis of race, religion,
color, national origin, sex, age, or disability with respect to access,
employment programs or services.
B. Students are urged not to bring children to either a class or a lab. Minors
under the age of twelve (12) must not be left unattended on campus. College
Academic Council - April, 1998
C. ADA Statement: “As per Section 504 of the Vocational Rehabilitation Act of
1973 and the Americans with Disabilities Act of 1990, if accommodation is needed
contact the Office of DisABILITY Support Services, CAC 124C, Phone: (210)
733-2347.
D. A Rapid Response Team exists for the purpose of responding to emergencies. If
you have a disability that will require assistance in the event of a building
evacuation, notify Disability Support Services, Chance Academic Center 124C,
Phone: (210) 733-2347.
E. Academic Dishonesty: Students may be subject to disciplinary proceedings
resulting
in an academic penalty or disciplinary penalty for academic dishonesty. Academic
Dishonesty includes, but is not limited to, cheating on a test, plagiarism and
collusion. For additional information refer to the “Student Code of Conduct” in
the San Antonio College Bulletin.
F. Students are required to silence all electronic devices (e.g., pagers,
cellular phones, etc.) when in classrooms, laboratories and the library. College
Academic Council, 01/ 2000.
G. San Antonio College Attendance Policy: Regular and punctual attendance at all
classes and laboratories, day and/or evening, is required. A student absent for
any reason is responsible for all work missed. Both tardiness and early
departure from class are forms of absenteeism. The instructor establishes the
policy with regard to each.
Absences of each student are recorded without exception. The counting of
absences begins on the first day of class. A student absent the equivalent of
two weeks of instruction in a 16-week semester may be dropped by the instructor.
If a student is dropped from a class for excessive absences, the instructor will
record a grade of “W’ (withdraw). It is the student’s responsibility to ensure
that the withdrawals have been submitted.
H. San Antonio College is a smoke free campus.
I. ACCD DPS Emergency Phone Numbers:
ACCD DPS Emergency Phone (210) 222-0911
ACCD DPS General Phone (210) 208-8099
ACCD DPS Weather Phone (210) 208-8189 (For information on college closures)
J. Students must also abide by the policies, procedures, and rules set forth in
the “Student Code of Conduct” and all other policies set forth in the San
Antonio College Bulletin. www.accd.edu/sa/sacmain/schedule/SAC_Bulletin_05-06.pdf
| Prev | Next |