Quadratic Functions and Parabolas
• Parabolas
• Quadratic equations and functions
• Graphs of quadratic functions
• Applications
Quadratic Functions and Expressions
A quadratic function has two forms:
• f(x) = ax^2 +bx+c (standard form)
• f(x) = a(x − h)^2 +k (vertex-axis form)
The graph of a quadratic function is a parabola. It is easy to
graph a quadratic function if it is expressed in the vertex-axis
form.
Graphing a quadratic function
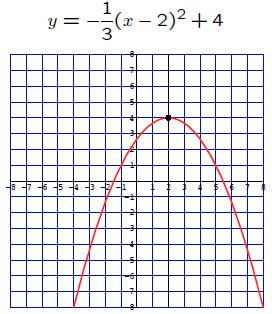
The vertex is the point at (2, 4)
The axis of symmetry is the vertical line x = 2
Graphing a quadratic function
y = 2(x+3)^2 − 5
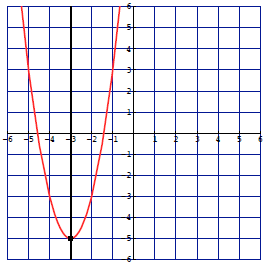
The vertex is the point at
The axis of symmetry is the vertical line
Graphing a quadratic function
The general case
y = a(x − h)^2 +k
The vertex is the point at (h, k)
The axis of symmetry is the vertical line
If a > 0, the parabola opens upward.
If a < 0, the parabola opens downward.
Questions:
• Does the graph of f(x) = 5(x − 1)^2 + 8 open upward or
downward?
• Does the graph of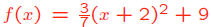 
open upward or
downward?
• What is the equation for the axis of symmetry for the graph
of f(x) = 5(x − 1)^2 +8?
• What are the coordinates of the vertex of the graph of
?
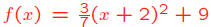Completing the square
How to change the standard form for the function into the vertexaxis
form.
Example: f(x) = x^2 − 6x+10
Change into vertex -axis form.
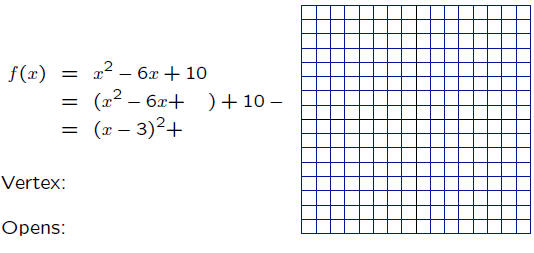
Problem: Change to vertex-axis form by completing the square:
f(x) = x^2 +4x − 5
Problem: Change to vertex-axis form by completing the square:
f(x) = −x^2 − 10x+1
Problem: Change to vertex-axis form by completing the square:
f(x) = 3x^2 +6x+1
Problem: Change to vertex-axis form by completing the square:
f(x) = 5x^2 − 30x+11
The general quadratic function:
f(x) = ax^2 +bx+c
The quadratic formula tells you the solutions to f (x) = 0,
which is the same as locating the x- intercepts on the graph :
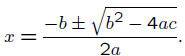
Example: Solve
2x^2 − 5x −3 = 0,
for x.
a = 2, b= −5, c = −3
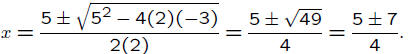
So x = 3 and x = 1/2 are the solutions .
Example: Solve
x^2 − 5x −5 = 0,
for x.
a = , b= , c =
| Prev | Next |