Adding and Subtracting Polynomials
Polynomials:
A term is defined as an expression containing a constant or the product of a
constant and one or more variables. Any term is made up of a number part
and a variable part .
Terms: 3x2 & −5 are two different terms. 3x2 − 5 is not
a term (it is two
terms).
A Polynomial is defined as a single term or the sum of two
or more terms
containing only whole number exponents on its variables.
Polynomials: 3x2 − 4x − 2 & 4xy2 + 3x2 − 3y + x − 2 are
polynomials.
Not Polynomials:
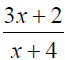& 3x-2 + 4x2 − 2 are not polynomials.
A monomial is a polynomial with one term, a binomial is a polynomial with
two terms , and a trinomial is a polynomial with three terms.
Give an example of a: Monomial:
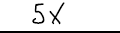
Binomial :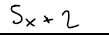
Trinomial :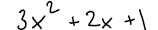
The degree of a term is the sum of the exponents on the variables.
Term:
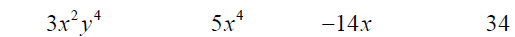
Degree: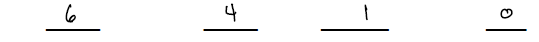
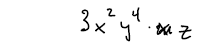
The degree of a polynomial is determined by the term with the largest
degree.
EXAMPLE: Determine the degree of the following polynomials:
A polynomial that is written in standard form will have its terms written so the
exponents will be in descending powers .
EXAMPLE: Write the polynomial in standard form:
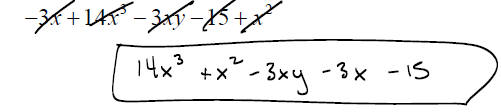
COMBINING LIKE TERMS (Review)
To add two objects, they must be of the same units. We can’t add feet and
inches because they don’t match. The same goes for terms. They must be
like terms .
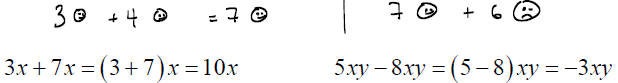
To add two like terms :
Combine their _______________, and leave the ____________part alone.
How do we combine unlike terms ? _________________
What is the opposite of −x3 + x2 − 3x + 5? ___________________
EXAMPLE: Perform the following operations
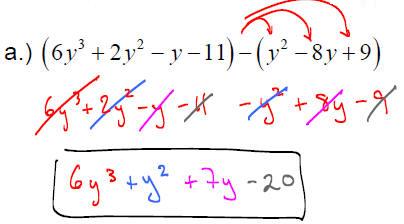
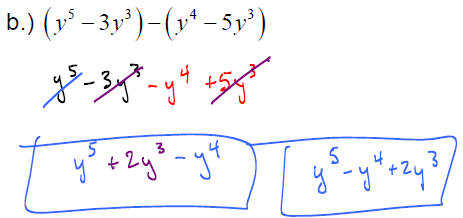
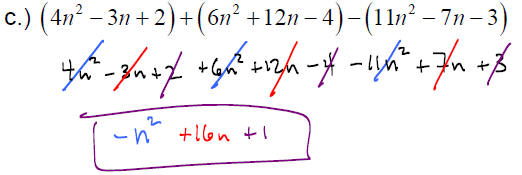
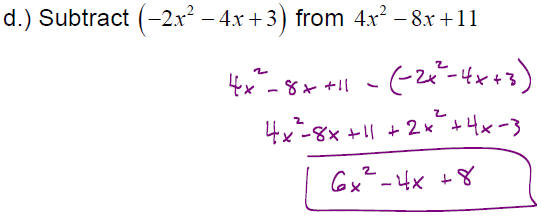
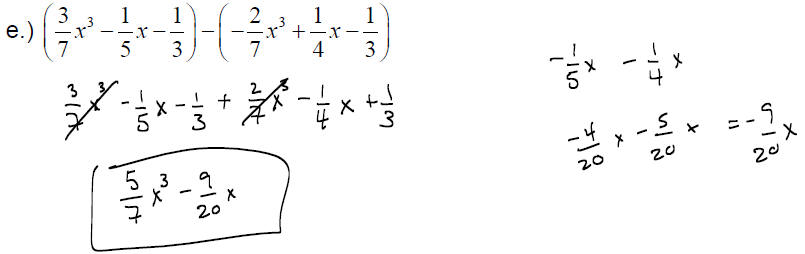
f.) Find the difference when 32x2 −17x + 45 is subtracted from the sum of
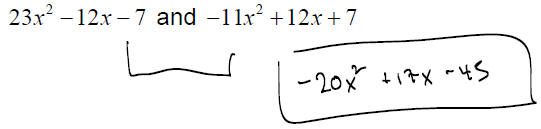
g.) (0.02x2 + x −.004) − (.01x2 + .0001x −.02)
| Prev | Next |