Math 237 Quiz 10

1. Prove the Solvability Criterion for Systems of Linear Equations.

Solution : The Solvability Criterion for Systems of Linear Equations
says that any system of linear equations AX = B is solvable if and only
if its vector of constants B belongs to the column space of its coefficient
matrix A (see Theorem 1 on p. 73 of the textbook). Suppose that A₁,
A₂, ..., A_n are the columns of A (in this order). Then

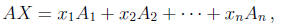
where 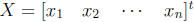(see p. 72 of the textbook). So if AX =
B is solvable , then B is contained in the span of the column vectors of A
(= column space of A) and conversely, if B is contained in the column
space of A, then 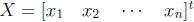is a solution of AX = B and
therefore AX = B is solvable .

2. Prove the Translation Theorem for Systems of Linear Equations .

Solution : The Translation Theorem for Systems of Linear Equations
says that S_B = T + S₀ for any particular solution T of the system
AX = B of linear equations . (Here S_B denotes the set of solutions of
the system AX = B and T + S₀ := {T + Z | Z ∈S₀} = {T + Z |
AZ = 0}.) Let us begin by proving the inclusion (see also the
footnote on p. 102 of the textbook). So suppose that S is any solution
of AX = B. Then A(S − T) = AS − AT = B − B = 0 shows
that S − T ∈S₀ or equivalently S ∈T + S₀. Now let us prove the
reverse inclusion 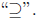So suppose that S = T + Z with Z ∈S₀. Then
AS = A(T + Z) = AT + AZ = B + 0 = B shows that S is a solution
of AX = B.