Quadratic Equations

Definition: A quadratic equation is an equation involving an
unknown to the second power (degree), but no higher power. The
general form of the quadratic equation is
ax ² + bx + c = 0, where x is the unknown and a ≠ 0.

The coefficient of the unknown of the highest exponent is called the
leading coefficient. For example, the leading coefficient of the
expression 7x² - 5x + 4 is 7, while the leading coefficient of the
expression 10+ 3u- 5u² is - 5.

Our first inclination is to think of quadratic as dealing with "four".
But the dictionary's definition of quadratic is "containing quantities of
the second degree". The name comes from "quadrature", an ancient
problem of constructing a square having the same area as the given
figure using only a compass and a straight edge. (To see that
quadrature is not such a simple problem , try constructing a square
having the same area as the rectangle whose length is 5 inches and
whose width is 2 inches, using only a compass and a straight edge.)

7.1 Solving Quadratic Equations by Factoring
To solve quadratic equations by factoring:
a) write the equation in standard form (bring all terms to the
left -hand side so that the right-hand side is zero),
b) factor the expression on the left (or right) side,
c) solve for the values of the unknown using the multiplication
property of zero .

Example 1: Find the solutions of the equation 2x² = 5x + 3 .

solution: 2x² - 5x - 3 = 0 bring all terms to the left-hand
side so that the
right-hand side is zero
(2x + 1)(x - 3) = 0 factor the trinomial
2x + 1 = 0 or x - 3 = 0 multiplication property of
zero
2x = - 1
So, and 3 are the solutions.[Note: Equation of degree 2
has , in general, 2 solutions.]

Example 2: Find the solutions of the equation 12n² = 9n .
solution: 12n² - 9n = 0 write equation in standard
form
3n(4n - 3) = 0 factor out common factors
3n = 0 or 4n - 3 = 0 set each factor equal to zero
The solutions are 0 and .

Example 3: Find the solutions: y² - 16 = 0
solution: y² - 16 = 0 the right-hand side is already
equal to zero
(y + 4)(y - 4) = 0 factor the difference of
squares
y + 4 = 0 or y - 4 = 0
y = - 4 or y = 4
The solutions are -4 and 4, which can also be written as .

Exercises 7.1
Solve the following quadratic equations by factoring:
(a) x² - 7x + 6 = 0
(b) n² + n = 6
(c) y² + 2y = 0
(d) 3m = m²
(e) 9t² - 1 = 0
(f) 4g² = 25
(g) 2a² = 5a - 3
(h) 3 + w = 2w²
(i) 12x² = 27
(j) 12x² = 27x
(k) 2n² + 10 = 12n
(l) 6y² = 6 - 5y
(m) (a - 3)(2a + 1) = 39
(n) 3p(2p - 1) = 18
(o) (4m - 3)(m - 2) = 6
(p) (2t + 5)(8t - 5) = 30t
(q) 6g² + 56 = 37g
(r) 1 = 64K²
(u) 0.09n² = 36
(v) y² - 20 = y

7.2 Solving Quadratic Equations by Extracting Roots
Recall the earlier section on the Pythagorean Theorem: a² + b² =
c². If a = 3 and b = 4, then

We took the square root (extracted the root) of 25 to get 5. But is 5
the only answer? If , then c = 5 or c = - 5 (since after squaring a
positive or a negative number, we always get a positive value). For
the problem above we were interested in the 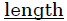of side c,
therefore, the positive value is automatically chosen. In this section,
we find ALL possible solutions--both positive and negative.

Equations of a more general forms x² - c = 0 or (ax - n)² - c = 0,
where c is a positive number, can be solved by root extraction.
Actually this method is an extension of the method covered in the
preceding section .

We have been saying that the expression is not factorable. The
statement is not entirely correct. We should say that is not
factorable using only integers. If we allow numbers like square
roots of positive numbers to be used , then the expression becomes
factorable because 3 can be written as , and so we can factor as
=
=

So, if we had the problem of finding all solutions of the equation , we
bring all terms to the left-hand side and factor the left-hand side, as in
the preceding section:
= 0

The solutions are and , which can be written as .

It is easy to see that we can replace 3 with any positive number. So,
we have the following result:

For any positive number a, if , then .

Example 1: Find the solutions: y² - 16 = 0
solution: isolate the squared variable
The solutions are .

Example 2: Solve the equation: 12n² - 9 = 0
solution: 12n² = 9 isolate squared term
The solutions are
and
, which can also be written as and.

Example 3 : Solve the equation: 3(x - 1)² = 24
solution: 3(x - 1)² = 24 squared quantity is isolated
(x - 1)² = 8
The solutions are and , which can also be written as
and .

"Why can't we use extraction of roots for other forms of the quadratic
equation?"
ax² + bx + c = 0: 2x² + 3x + 1 = 0
2x² = - 3x - 1

ax² + bx = 0: x² - 5x = 0
x² = 5x

Exercises 7.2
Solve the following quadratic equations by extracting roots:
(a) x² - 4 = 0
(b) n² = 25
(c) p² - 2 = 0
(d) m² = 7
(e) a² - 12 = 0
(f) K² = 27
(g) 2y² - 98 = 0
(h) 3z² = 48
(i) 3w² = 30
(j) 2t² - 126 = 0
(k) 5x² = 1
(l) 2a² - 7 = 0
(m) 4p² = 1
(n) 25m² = 9
(o) 12k² - 5 = 0
(p) 24z² = 8
(u) 2(7w + 3)² = 128
(v) 3(2y - 5)² = 24

7.3 Solving Quadratic Equations by the Quadratic
Formula
The quadratic formula can be derived by solving the general
quadratic equation
ax² + bx + c = 0 using the method known as completing the square
(which is not discussed here).

When a procedure is often repeated, mathematicians prefer to use a
formula to shorten the number of steps . Use of the quadratic formula
produces results more quickly than by the method of completing the
square. In using the formula, you want to:
a) write the equation in standard form,
b) correctly identify a, b, and c,
c) carefully substitute into the formula .

Example 1 : Find the solutions of the equation x² + 4x - 6 = 0
Solution: x² + 4x - 6 = 0 equation is in standard form;
hence, a = 1, b = 4, c = - 6

Therefore, .

Example 2: Find the solutions of the equation: 2n² = n + 3
Solution: 2n² - n - 3 = 0 write the equation in
standard form   and substitute
into the formula

[Note: When the solutions are rational (as in this case), the equation
could have been solved by factoring. Try this and see if you obtain
the same results.]

Example 3: Solve the equation: 2 + 2w + w² = 0
Solution: w² +2w + 2 = 0 write the equation in standard
form and
substitute into the formula

But, since the square root of - 4 is not a real number
we say that there are no real solutions.

In the previous examples, we used the formula with equations whose
left-hand side contained a trinomial expression. What if the left-hand
side is a quadratic binomial ?

Example 4: Solve the equation: 8x² + 4x = 0
Solution: If we wish to use the quadratic formula, then a = 8, b = 4,
and c = 0.

But since the left-hand expression is easily factorable,
there is no need to   use the formula.
4x(2x + 1) = 0
4x = 0 or 2x + 1 = 0

Example 5 : Solve the equation: 12y² - 9 = 0
Solution: If we wish to use the quadratic formula, then a = 12, b =
0, and c = - 9.

But since we can use the extraction of roots method, there
is no need to use   the formula.

Although the quadratic formula can be used to solve all quadratic
equations, it is often the most time-consuming. We usually reserve
the use of the quadratic formula for those situations when factoring
or extracting roots do not work.

Exercises 7.3
Solve the following quadratic equations by the most effective method.
(a) x² - 8x + 15 = 0
(b) 2n² + 3n = 2
(c) 6y² - 14y = 0
(d) 6z² = 48
(e) 2a² = 3a + 1
(f) m² + 10m = 4
(i) n² + 8n = 1
(j) 2z² = 3z - 8
(k) 4a² + 5a = 0
(l) 3m² + 4m = 3
(m) 4t² = 4t + 7
(n) 12w² - 27 = 0
(o) x² - 2x = 5 + 2x
(p) 2y² + 2y - 3 = 5 - y²
(q) (n + 1)² = 2 - 4n
(r) (2x - 1)² = 12
(s) (2x + 1)² = 2 + 8x
(t) 2(w - 1)² = 7w