Zeros of Polynomials

In Exercises 1-6, use direct substitution
to show that the given value is a
zero of the given polynomial.
1. p(x) = x³ − 3x² − 13x + 15, x = −3
2. p(x) = x³ − 2x² − 13x − 10, x = −2
3. p(x) = x⁴ − x³ − 12x², x = 4
4. p(x) = x⁴ − 2x³ − 3x², x = −1
5. p(x) = x⁴ + x² − 20, x = −2
6. p(x) = x⁴ + x³ − 19x² + 11x + 30,
x = −1

In Exercises 7-28, identify all of the
zeros of the given polynomial without
the aid of a calculator . Use an algebraic
technique and show all work (factor
when necessary) needed to obtain the
zeros.
7. p(x) = (x − 2)(x + 4)(x − 5)
8. p(x) = (x − 1)(x − 3)(x + 8)
9. p(x) = −2(x − 3)(x + 4)(x − 2)
10. p(x) = −3(x + 1)(x − 1)(x − 8)
11. p(x) = x(x − 3)(2x + 1)
12. p(x) = −3x(x + 5)(3x − 2)
13. p(x) = −2(x + 3)(3x − 5)(2x + 1)
14. p(x) = 3(x − 2)(2x + 5)(3x − 4)
15. p(x) = 3x³ + 5x² − 12x − 20
16. p(x) = 3x³ + x² − 12x − 4
17. p(x) = 2x³ + 5x² − 2x − 5
18. p(x) = 2x³ − 5x² − 18x + 45
19. p(x) = x⁴ + 4x³ − 9x² − 36x
20. p(x) = −x⁴ + 4x³ + x² − 4x
21. p(x) = −2x⁴ − 10x³ + 8x² + 40x
22. p(x) = 3x⁴ + 6x³ − 75x² − 150x
23. p(x) = 2x³ − 7x² − 15x
24. p(x) = 2x³ − x² − 10x
25. p(x) = −6x³ + 4x² + 16x
26. p(x) = 9x³ + 3x² − 30x
27. p(x) = −2x⁷ − 10x⁶ + 8x⁵ + 40x⁴
28. p(x) = 6x⁵ − 21x⁴ − 45x³

In Exercises 29-34, the graph of a polynomial
is given. Perform each of the following
tasks.

i. Copy the image onto your homework
paper. Label and scale your axes,
then label each x- intercept with its
coordinates.
ii. Identify the zeros of the polynomial.
29.

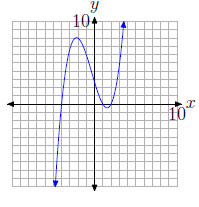
30.

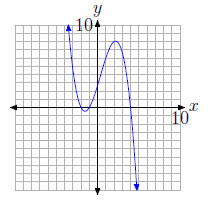
31.

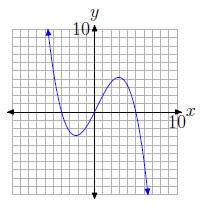
32.

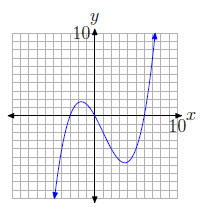
33.

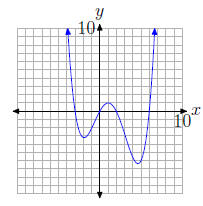
34.

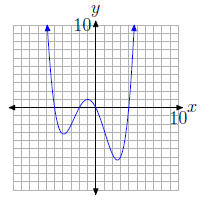
For each of the polynomials in Exercises 35-
46, perform each of the following tasks.

i. Factor the polynomial to obtain the
zeros. Show your work.
ii. Set up a coordinate system on graph
paper. Label and scale the horizontal
axis. Use the zeros and end-behavior
to help sketch the graph of the polynomial
without the use of a calculator.
iii. Verify your result with a graphing calculator.
35. p(x) = 5x³ + x² − 45x − 9
36. p(x) = 4x³ + 3x² − 64x − 48
37. p(x) = 4x3 − 12x² − 9x + 27
38. p(x) = x³ + x² − 16x − 16
39. p(x) = x⁴ + 2x³ − 25x² − 50x
40. p(x) = −x⁴ − 5x³ + 4x² + 20x
41. p(x) = −3x⁴ − 9x³ + 3x² + 9x
42. p(x) = 4x⁴ − 29x² + 25
43. p(x) = −x³ − x² + 20x
44. p(x) = 2x³ − 7x² − 30x
45. p(x) = 2x³ + 3x² − 35x
46. p(x) = −2x³ − 11x² + 21x

6.2 Solutions
1. p(−3) = (−3)³ − 3(−3)² − 13(−3) + 15 = −27 − 27 + 39 + 15 = 0
3. p(4) = 4⁴ − 4³ − 12(4)² = 256 − 64 − 192 = 0
5. p(−2) = (−2)⁴ + (−2)² − 20 = 16 + 4 − 20 = 0
7. Set p(x) = 0 in p(x) = (x − 2)(x + 4)(x − 5),
0 = (x − 2)(x + 4)(x − 5),

then use the zero product property to write
x − 2 = 0 or x + 4 = 0 or x − 5 = 0.

Solving , the zeros are x = 2, −4, and 5.

9. Set p(x) = 0 in p(x) = −2(x − 3)(x + 4)(x − 2),
0 = −2(x − 3)(x + 4)(x − 2),

then use the zero product property to write
x − 3 = 0 or x + 4 = 0 or x − 2 = 0.

Solving , the zeros are x = 3, −4, and 2.

11. Set p(x) = 0 in p(x) = x(x − 3)(2x + 1),
0 = x(x − 3)(2x + 1),

then use the zero product property to write
x = 0 or x − 3 = 0 or 2x + 1 = 0.

Solving, the zeros are x = 0, 3, and −1/2.

13. Set p(x) = 0 in p(x) = −2(x + 3)(3x − 5)(2x + 1),
0 = −2(x + 3)(3x − 5)(2x + 1),

then use the zero product property to write
x + 3 = 0 or 3x − 5 = 0 or 2x + 1 = 0.

Solving, the zeros are x = −3, 5/3, and −1/2.

15. Factor p(x) = 3x³ + 5x² − 12x − 20 by grouping, then finish the factoring using
the difference of squares pattern.
p(x) = 3x³ + 5x² − 12x − 20
p(x) = x²(3x + 5) − 4(3x + 5)
p(x) = (x² − 4)(3x + 5)
p(x) = (x + 2)(x − 2)(3x + 5)

To find the zeros, set p(x) = 0,
0 = (x + 2)(x − 2)(3x + 5),

then use the zero product property to write
x + 2 = 0 or x − 2 = 0 or 3x + 5 = 0.

Solving, the zeros are x = −2, 2, or −5/3.

17. Factor p(x) = 2x³ +5x² −2x−5 by grouping, then finish the factoring using the
difference of squares pattern .
p(x) = 2x³ + 5x² − 2x − 5
p(x) = x²(2x + 5) − 1(2x + 5)
p(x) = (x² − 1)(2x + 5)
p(x) = (x + 1)(x − 1)(2x + 5)

To find the zeros, set p(x) = 0,
0 = (x + 1)(x − 1)(2x + 5),

then use the zero product property to write
x + 1 = 0 or x − 1 = 0 or 2x + 5 = 0.

Solving, the zeros are x = −1, 1, or −5/2.

19. Start with p(x) = x⁴ + 4x³ − 9x² − 36x. Factor out the gcf (x in this case), then
factor by grouping . In the last step, use the difference of squares pattern to complete
the factorization.
p(x) = x[x³ + 4x² − 9x − 36]
p(x) = x[x²(x + 4) − 9(x + 4)]
p(x) = x(x² − 9)(x + 4)
p(x) = x(x + 3)(x − 3)(x + 4)

Set
0 = x(x + 3)(x − 3)(x + 4)

and use the zero product property to write
x = 0 or x + 3 = 0 or x − 3 = 0 or x + 4 = 0.

Solving, the zeros are x = 0, −3, 3, and −4.

21. Start with p(x) = −2x⁴ − 10x³ + 8x² + 40x. Factor out the gcf (−2x in this
case), then factor by grouping. In the last step , use the difference of squares pattern
to complete the factorization.
p(x) = −2x[x³ + 5x² − 4x − 20]
p(x) = −2x[x²(x + 5) − 4(x + 5)]
p(x) = −2x(x² − 4)(x + 5)
p(x) = −2x(x + 2)(x − 2)(x + 5)

Set
0 = −2x(x + 2)(x − 2)(x + 5)

and use the zero product property to write
−2x = 0 or x + 2 = 0 or x − 2 = 0 or x + 5 = 0.

Solving, the zeros are x = 0, −2, 2, and −5.

23. Start with p(x) = 2x³ − 7x² − 15x. Factor out the gcf (x in this case), then use
the ac- method to complete the factorization.
p(x) = x[2x² − 7x − 15]
p(x) = x[2x² − 10x + 3x − 15]
p(x) = x[2x(x − 5) + 3(x − 5)]
p(x) = x(2x + 3)(x − 5)

Set
0 = x(2x + 3)(x − 5)

and use the zero product property to write
x = 0 or 2x + 3 = 0 or x − 5 = 0.

Solving, the zeros are x = 0, −3/2, and 5.