Study Guide for Math 120 Midterm One

The midterm is 85 minutes long and will be given on Wednesday, February 25, 2008 at the beginning of class. Please arrive early so that we can start on time. The test will cover chapters 3, 8, and sections 10.1 - 10.3 of the text. To study for this test, go through your homework, class handouts, and class examples. You will be allowed to use your calculator for the test . You may not share calculators or use mine. Please seek help in the Math Lab and Learning Center early and frequently.

Be familiar with the instructions specified in the textbook exercises. The wording on the test will be similar. It is important to not just know how to do a problem, but to understand what exactly the problem is asking you to do.

Any use of other electronic devices such as cell phones and mp3 players will result in a 0 on the exam.

The problems shown are only examples – refer to your text for additional problems to work on.
• Know how to use function notation and write your answers as ordered pairs .
1. Find f(3) when f(x) = 3x² – 8x + 9. Write your answer as an ordered pair.
2. Find f(−3) when f(x) = 2x² +9x −4. Write your answer as an ordered pair.

• Identify the domain and range of a relation or function and write your answer in set-builder notation.
3. Find the domain and range of the relation {(9,3),(5,3),(4,2),(−8,1)}. Write your answer in set-builder notation.
4. Find the domain and range for the function f(x) = 3x – 7. Write your answer in set-builder notation.
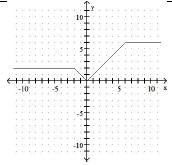
5. Find the domain and range of the function graphed to the right. Write your answer in set-builder notation.

• Given a word problem, be able to clearly define your variables, extract the facts, make predictions , and interpret the meanings of the slope and different ordered pairs in the context of the problem.
6. The number of people employed in the United States as systems analysts was 431 thousand in 2000. By the year 2010, this number is expected to rise to 689 thousand. Let y be the number of systems analysts (in thousands) employed in the United States in the year x, where x = 0 represents 2000.
Remember to clearly define your variables!
a) Write a linear function that models the number of people (in thousands) employed as systems analysts
b) Use this function to estimate the number of people who will be employed as systems analysts in the year 2008.

• Recognize linear and non -linear functions and graph them.
8. Use the given graph to answer the questions

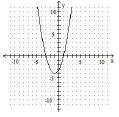
a) Find f(−1). Write your answer as an ordered pair.
b) Find all x-values such that f(x) = 5
9. Graph each function.
a) f(x) = x² + 3
b) h(x) = |x| − 5
c) k(x) = (x – 4)²+ 1

• Algebra of functions: sum , difference, product, and quotient of functions as well as composite functions. Also, given a function, be able to determine two functions whose composition results in that function.
10. Use the given functions to answer the questions that follow
f(x) = x² – 2 and g(x) = 3x + 1
a) Find (f + g)(x)
b) Find (f – g)(x)
c) Find (f ∙ g)(x)
d) Find (f/g) (x)
e) Find (f ° g)(x)
11. Use the given functions to answer the questions that follow. f(x) = 2x − 3, g(x) = x + 5, and h(x) = |x|
a) Write the function G(x) = 2x + 7 as a composition of f, g, or h.
12. Find f(x) and g(x) so that the given function h (x) =(f ° g)(x)
a) h(x) = (x + 3)²
b) h(x)= (3x + 4)² + 3
13. Given the values below, find each function value.

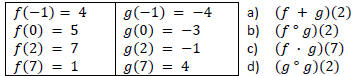
• Direct and inverse variation problems (8.4).
14. At sea, the distance to the horizon is directly proportional to the square root of the elevation of the observer. If a person who is 36 feet above the water can see 7.4 miles, find how far a person 64 feet above the water can see. Round your answer to one decimal place.
a) Underline the sentence that you will be translating & identify the type of variation.
b) Clearly define your variables.
c) Solve for k and give the general formula .
d) Solve the problem. Show your work and write your answer in a complete sentence.

• Radicals and rational exponents
15. Use the properties of exponents to simplify the expression. Write with positive exponents.

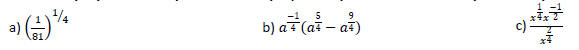
16. Use radical notation to write the expression. Then simplify your answer .

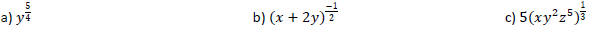
17. Multiply

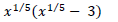
18. Factor the common factor from the given expression

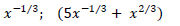
19. Use rational exponents to simplify each radical. Assume that all variables represent positive numbers.

20. Use rational expressions to write as a single radical expression.