Math 90 Chapter 7 Lecture Notes

Section 7.2: Systems of Equations and Substitution

The method of substitution for solving systems of linear equations works for any
linear system , but works best if one of the equations in the system can easily be
solved for one of the variables. What we look for in particular is a variable in
either equation that has a coefficient of 1. This makes the substitution method very
easy to use. Work through the following examples to see how easy this method is
to use. Remember that we are trying to find a point where the two lines intersect,
and a point has both an x and a y coordinate .

A. Some sample problems: Solve using the method of Substitution.

1. 2x + y = 1
x – 5y = 17

2. 2x – 4y = -4
x + 2y = 8

3. 7x + 6y = -9
y = -2x + 1

B. Remember that not all systems of linear equations have one unique solution.
What are the other cases?

1. If the lines are parallel, how many solutions will you find? ______

2. If the lines coincide, how many solutions will you find? _______ .

C. Some rules for solving systems of linear equations

5. If possible, remove by factoring, any constant multiplier that may be in
the equations. This action will not change the equality but will make the
equation simpler.
6. Re-arrange the equations such that both are in the same form. For
instance place all terms on the left with zero on the right.
7. If the two equations are identical, then these equations lie one on top of
the other and there are an infinite number of solutions .
8. If the variable terms are identical but the constants different then these
are parallel lines and there is no solution.
9. If options 3 and 4 are both false then there is one solution.

D. Work through the following examples to see what happens when you encounter
one of the situations described above:

E. Some examples of application problems:

1. Find two numbers such that the sum is 76 and the difference
is 12.

2. Two angles are supplementary. One angle is 8 degrees less than
three times the other . Find the measure of each angle.

3. The state of Wyoming is a rectangle with a perimeter of 1280
miles. The width is 90 miles less than the length. Find the length
and the width.

Section 7.3: Systems of Equations and Elimination

In this section we will learn another method for solving systems of equations called
the Elimination Method. In this method, you want to ultimately add the two
equations together and eliminate one of the variables. Work through the following
examples to see how this is done.

A. The Rational behind this method: Note the following:

If A = B and
C = D then it is true that: A+C = B+D

Because of this fact, we can always add two equations together to get another
true equation. We will use this fact when we use the elimination method for
solving systems of equations.

B. Some sample problems: Solve the following using the Elimination Method. But
before solving these equations let us examine them to determine what kind of
solution we can expect.

1. x – y = 1
-x – y = -7

2. x – y = 4
2x + y = 8

3. –x + 10y = 1
-5x + 15y = -9

4. 2x + 9y = 2
5x + 3y = -8

C. Once again remember that not all systems of equations have a unique solution.
Follow the next two examples to see what happens when we get no solution, or
an infinite number of solutions.

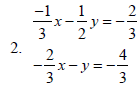How many solutions does this system have?

Section 7.4: More Applications using Systems

In this section we will practice solving application problems using systems of
equations. The most important part of this process is setting up the system that
models the situation. You can use either the substitution method or the elimination
method to solve the system that you set up.

A. Sample application problems:

1. In winning the 2000 conference finals, the Los Angeles Lakers
scored 69 of their points on a combination of 31 two and three
pointers. How many of each type of shot did they make?

2. Filmworks charges $1.75 for a role of 24-exposure film and $2.25
for a 36-exposure roll of film. Stu bought 19 rolls of film for a
total of $39.25. How many rolls of each type did he buy?

3. From November 2 through January 3, the Bronx Zoo charges $6.00
for adults and $3.00 for children and seniors. One December day,
a total of $1554 was collected from 394 admissions. How many
adult and how many children/senior admissions were there?

4. Sunflower seed is worth $1.00 per pound and rolled oats are
worth $1.35 per pound. How much of each would you use to make
50 pounds of a mixture worth $1.14 per pound.

5. Clear Shine window cleaner is 12% alcohol and Sunstream
window cleaner is 30% alcohol. How many ounces of each should
be used to make 90 ounces of a cleaner that is 20% alcohol?

Section 7.5: Linear Inequalities in Two Variables

In this section we will learn how to find solutions of linear inequalities in two
variables.

A. An example of an inequality in one variable. Solve and graph the
solution set for the following inequality:

3(x + 5) ≤ 22

Note: There are an infinite number of solutions to this inequality. Because of this
we need to describe our solutions and/or graph them as it would be impossible to
list them all.

B. Find and graph as many ordered pair solutions to the following
inequality.

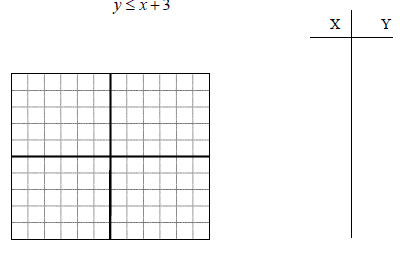
C. What do you notice about the boundary for the solutions to this
inequality in two variables?

1. _________________________________________________

2. _________________________________________________

D. Graph the solution set for the following inequalities in two variables:

1. y ≤ 3x + 2

2. 5x + 4y ≥ 20

Remember that when you are graphing the solution set to an inequality in two
variables that you must first graph the “Boundary Line”. The boundary line will be
solid when: ______________________ , and the boundary line will be dashed or
dotted when: _______________________ .