Slopes and Lines

Get into groups of three or four and work on the following. Elect one person to write up your
answers neatly and turn the worksheet in on Monday. You may need to arrange a meeting
outside of class, so consider exchanging contact information. If you need to remind yourself
about lines, read section §1.4 or take a look at the material online under the Absolute &
Lines assignment .

1. Shape: Let f(x) = mx where m is some constant

(a) If m =-2, write down the explicit rule for f . Hint: f(x) =?

(b) Plot some points and sketch the graph of f when

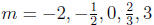
(c) For each graph above , determine if the graph defines a function.
(d) For each function graphed above, find the domain and range.
(e) For each graph above, find the x and y intercepts.
(f) On the graphs above, find the intervals that the graphs are increasing and decreasing.
(g) Determine if the graph of f is increasing, decreasing, or doing neither if:
 •m > 0:
 •m = 0:
 •m < 0:

2. Slope: Let m be a fixed rational number .

(a) Explain (in English) what the slope of a line is.

(b) Given two points : (a, b) and (c, d) on a line, explicitly find a formula for the slope.

(c) Let g(x) = mx, and recall that m is a fixed rational number . Find two points
that are on the line of the graph of g. (Recall the definition of a graph. What
would the y coordinate be if the x was 1? 0?)

(d) Use the formula you created in (b) along with the two points you found in part (c) to find the slope of the graph of g where g(x) = mx.

(e) Let b be a number, and h(x) = mx + b. The graph of h is increasing, decreasing, or doing neither if:

 •m > 0:
 •m = 0:
 •m < 0:

Hint: Choose some numbers, graph them, and try to find a pattern to the data.
The rule of the function h is a special form called slope intercept form . Why does
it have this name?

(f) Let the graph of the function be a line with slope -1/3 and assume the graph
crosses the y-axis at (0, 7). Find the rule of α.

(g) Let the graph of the function be a line with slope 1/2 and assume it passes through
the point (3, 2). Find the rule of β.

Hint: Since you know what m is, write β(x) = mx + b, and try to solve for b by
plugging in points. Otherwise, there is a "point-slope formula" that can be used.

(h) Let the graph of the function γ be a line that passes through the points (-1, 2)
and (2,-4), find the rule of γ.

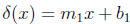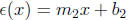(i) Consider the graphs of two functions : and with
slopes m₁ and m₂, respectively. If 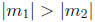, which graph is steeper?

(j) Special Cases: What is the slope of a horizontal line? A vertical one? In each
case, is the line the graph of a function?

3. Parallel Lines

(a) Explain (in English) what parallel lines are

(b) If two lines are parallel, what is the relationship between their slopes?

(c) Using the observation above, is a line parallel to itself?

4. Perpendicular Lines

(a) Explain (in English) what it means for two lines to be perpendicular. Be specific.

(b) If two lines are perpendicular, what is the relationship between their slopes?

(c) Find the equation of a line perpendicular to the line through (-2,-1) and (4, 3).
Note: There are many right answers.

(d) (a great idea that is best worked through when I am there) Prove if f(x) = mx+b,
then a non-vertical or horizontal line is perpendicular if it has slope equal to -1/m.

 • Draw a pair of non-vertical perpendicular lines which intersect at the origin.
Label one M and the other K. (Consider the lines as graphs of the functions,
M(x) and K(x).)

 •Draw, on the graph above, the vertical line x = 1. Label each of the intersections you've just created: (1,m) and (1, k) for the lines M and K respectively.
 • Calculate the slopes of the lines M and K.
 •Using the length formula on page 38, calculate the length from (0, 0) to (1,m).
 •Calculate the length from (0, 0) to (1, k).
 •Calculate the length from (1,m) to (1, k).
 •Note the triangle formed by (0, 0), (1,m), and (1, k) is a right triangle. Use the lengths calculated above and the Pythaogrean Theorem to solve for m.