Polynomial Functions

Example 1: A rectangle has a perimeter of 40 ft. What is the maximum area of the rectangle?

Assign the width of the rectangle the variable x. The sum of the length and the width is 20. So in
terms of x, the length is 20 − x . The function A (x) = the area of the rectangle depending upon its
width:

A (x) = x (20 − x)

Remember, that area = width · length.

Now to find its maximum value, find its vertex:

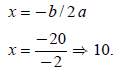
The above is the x- coordinate of the vertex . The following is the y-coordinate of the vertex, the
maximum value:

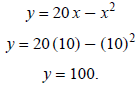
The maximum area is 100 ft² when the length and width are 10 ft each.

Example 2: Let's try problem 12 on page 72.

Let I (d) = the income for the fruit based on the days waited:

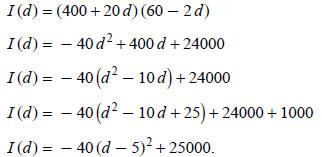
The vertex is (5, 25000).

The grower should wait 5 days. The maximum income is $25,000.

Example 3: Try problem 4 on page 73 of your text.

If the perimeter is 30 in, then the sum of the length and width is 15. The entire width is 3 x, so the
length is 15 − 3 x. The length of the rectangle becomes the height of the prism. To find the volume
of a prism, you find the area of the base, the equilateral triangle, and multiply it by the height of the
prism, 15 − 3 x. From geometry, we know each angle of an equilateral triangle measures 60°. The
altitude is the height of the triangle, and it will bisect the third side. The triangle formed by drawing
the altitude has angle measurements of 30°, 60°, and 90°. The length of the altitude is found by
multiplying half the base, .5 x, by .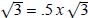

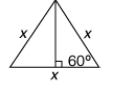
Now find the area of the triangle:

Area = .5 (base) (height).

Area of triangular base is

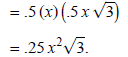
The volume of the prism = area of base× height:

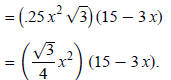
The domain of V (x) consists of the values of x that can be used in the function. Because x represents
one side of the triangular base, it can't be less than or equal to zero. Also, 15 − 3 x represents the
height of the prism, 15 − 3 x > 0: 0 < x < 5.

If you have a graphing calculator, graph the function and trace the values of x and y within the range
0 < x < 5. What would be the maximum volume, or the largest value of y?

Study Exercises

Complete odd- numbered problems 1–7 in the Written Exercises section on page 71 of your text.
Then check your answers in the back of the text.

Section 2-5: Using Technology to Approximate Roots of Polynomial Equations
pp. 75–80

We have discussed that roots of polynomial equations can be found by factoring, using synthetic
division, and by graphing. In this section, we will use the LOCATION PRINCIPLE to approximate
roots.

The idea behind the location principle is that zero is between positive and negative numbers. So if
you place values into a function and the value of the function changes in sign, the function had a
value of zero between the two values . Your text gives a program you can type into a programmable
calculator to find several function values. If your calculator is not programmable, you can keep
entering values into the function and keep a chart of the values.

Example 1: Let's try just one problem, problem 16 on page 78 of your text.

If all faces of the cube have x cm shaved off, all dimensions will be decreased by 2 x. The original
volume was 3×5×4 = 60 cm³. We are looking for the number of centimeters shaved off to give
half of that volume, 30 cm³. Let V (x) = the volume of a cube when x cm is shaved off each face:

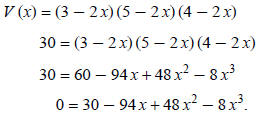
The domain is 0 < x < 1.5, because you cannot shave 1.5 cm or more from each side of a 3-cm
length, the smallest dimension. We are looking for an x-value that will produce V (x) = 0. A table of
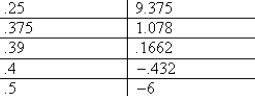
values follows.

x-value	V(x)-value

You can see by looking at the table that the value of V (x) changed in sign between V (.25) and
V (.5). So I keep trying x-values between .25 and .4. The directions in your text state to find a value
approximated to the nearest hundredth. I found that V (x) has a zero-value .39 < x < .4, and V (.39) is
closer to zero than V (.4). Each face of the solid will need to be shaved .39 cm to obtain a
rectangular solid half its original volume.

Study Exercises

Complete odd-numbered problems 1–15 in the Written Exercises section on page 78 of your text.
Then check your answers in the back of the text.

Section 2-6: Solving Polynomial Equations by Factoring, pp. 80–85

Factoring is a very powerful tool for finding roots of polynomial equations. Some polynomial
equations of a degree higher than two can be factored by grouping or by ordinary factoring methods.

Example 1: Solve 4 x³ + 3 x² − 36 x − 27 = 0.

Factor by grouping into two sets of binomials :

(4 x³ + 3 x²) + (−36 x − 27) = 0.

Factor out the GCF of each binomial :

x² (4 x + 3) − 9 (4 x + 3) = 0.

Notice a GCF of (4 x + 3). Factor it out:

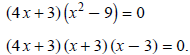
The solutions are 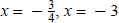, and x = 3.

Example 2: Solve x³ − x² = 20 x:

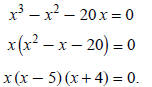
The solutions are x = 0, x = 5, and x = − 4.

Example 3: Solve 8 (2 x + 1)² + 10 (2 x + 1) = 3:

8 (2 x + 1)² + 10 (2 x + 1) − 3 = 0.

This equation can be written in quadratic form if 2 x + 1 is replaced by y.

Factor:

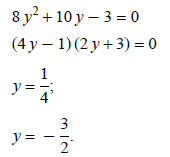
Replace y with 2 x + 1:

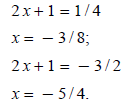
Example 4: Solve 4 x⁶ + 17 x³ − 15 = 0.

This equation can be written in quadratic form if x³ is replaced by y:

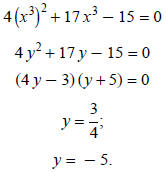
Replace y with x³:

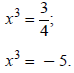
Take the cube root of both sides:

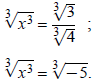
Rationalize the denominator in the first solution by multiplying by :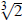

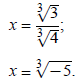
The solutions are

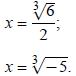
Let's examine 18 x² + 3 x − 10 = 0 closely. It can be factored as (6 x + 5) (3 x − 2) = 0. The solutions
are 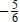and 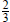. Note the factors of 18 (6 and 3) are in the denominators of the solutions. Also the
factors of 10 (5 and 2) are in the numerators of the solutions . If you were trying to find solutions to
an equation you were not capable of factoring, you could make a list of possible rational roots. The
possible rational roots have factors of the leading coefficient in the denominators and factors of the
constant term in the numerators. The RATIONAL ROOT THEOREM states that fact.