GCF and Factoring by Grouping
The greatest common factor , or GCF, is the largest factor
each term has in common. The
GCF can include numbers and variables . In terms of numbers, it is the largest
factor each
number has in common . For example, 4 is the greatest common factor of the two
numbers 4 and 20. (Notice that 2 is also a common factor ; however, it is not the
greatest
common factor.) In terms of variables , the GCF is the largest exponent each
variable has
in common . For example, x3 is the greatest common factor of x3
and x5 . (Again, x is a
common factor; however, it is not the greatest common factor).
We can factor a polynomial using the GCF (this means we are going to do a
reverse
distributive property ). Remember distributive property means multiplication, so
the
reverse is division . Factoring is a form of division.
Example 1: Factor out the GCF: 15x3 + 9x2
Solution : The GCF is 3x2 (3 is the common factor between 15
and 9 and x2 is the
common factor between x3 and x2 . We factor out 3x2
from each term to get
3x2 (5x + 3 ). You can check your answer by performing distributive
property (you
should get the original problem).
Example 2: Factor out the GCF: 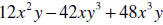
Solution: The GCF is 6xy . We will factor 6xy from each term to get
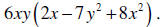
Factoring by grouping is used when there is four terms in the polynomial. We
will group
the first two terms and factor out the GCF then group the next two terms and
factor out
the GCF. We will have gone from four terms to two terms and factor out what is
common. Again, we will be doing reverse distributive property.
Example 3: Factor 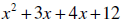
Solution: There are four terms; therefore, we will separate the first two
terms from the
next two terms and find the GCF of each pair .
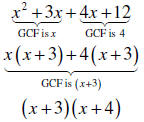
Example 4: Factor
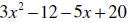
Solution: Again, there are four terms; therefore, we will factor by
grouping. Any time
you factor by grouping, it is not a coincidence the two terms have the same
factor in
parentheses. You always want the same binomial in parentheses in the second
step .
Practice Problems
Factor the Greatest Common Factor (GCF)

Factor by grouping
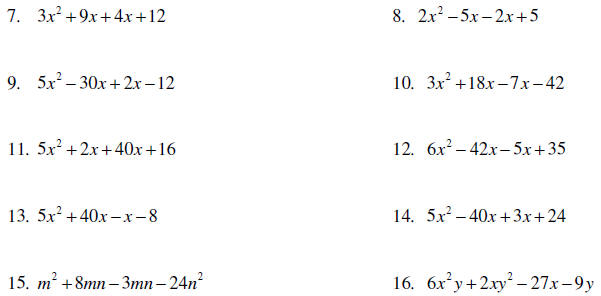
| Prev | Next |