Mathematics 106 Problem Set Solutions
1. Find an equation for the line with x - intercept 20 and
y -intercept 5. Sketch its graph.
Solution : It goes through (20, 0) and (0, 5), so it has slope
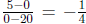. Its equation
may be written as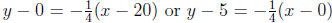 
. Its graph may be drawn
by simply connecting the two intercepts with a straight line.
2. Factor x 3 + 3x2 − 34x − 120 completely.
Solution : Looking at the divisors of 120, we see −4 is a zero of the
polynomial, so
x−(−4) = x+4 is a factor. Factoring x +4 out (using long division , synthetic
division
or some other method ), we get x3 + 3x2 − 34x − 120 = (x + 4)(x2 − x − 30).
The second factor may be further factored at sight or by trial and error to get
x3+3x2−
34x − 120 = (x + 4)(x + 5)(x − 6).
3. For what values of x is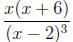 
negative?
Solution: We note the numerator is 0 when x = 0 and when x = −6 and the
denominator
is 0 when x = 2.
When x > 2, all the factors are positive so the quotient is positive.
When 0 < x < 2, x − 2 < 0, so (x − 2)3 < 0, but the other factors are positive
so the
quotient is negative.
When −6 < x < 0, x < 0, (x − 2)3 is still negative, while x + 6 > 0, so the
quotient is
positive .
When x < −6, x+6 < 0 and x and (x−2)3 remain negative, so the quotient is
negative.
We conclude 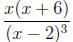is negative when x < −6 and when
0 < x < 2. We may describe
the set for which 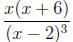is negative as {x|x < −6
or 0 < x < 2} = (−∞,−6) ∪ [ (0, 2).
4. Calculate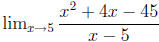 
.
Solution: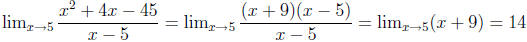 
.
5. The distance s (in feet) traversed along a straight
path by an object by time t (in seconds)
is given by the formula s = 8t3 + 5t2 + 2t.
(a) Find its average speed during the time interval 2 ≤ t ≤ 4.
Solution: Its average speed is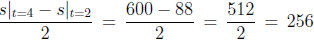 
feet per
second.
(b) Find its instantaneous speed when t = 3.
Solution: Its instantaneous speed i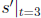s 
. s' = 24t2+10t+2, so its
instantaneous
speed is 248 feet per second.
6. Let f(x) = x3 + 5x. Use the definition of a derivative to find f'(x).
Solution: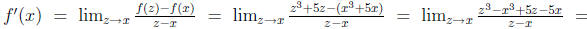
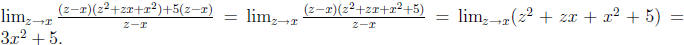
7. Calculate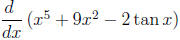 
.
Solution: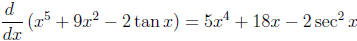 
8. Calculate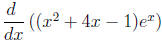 
Solution: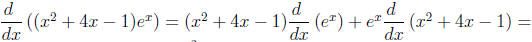
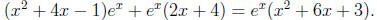
9. Calculate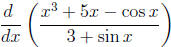 
.
Solution: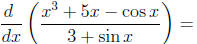 
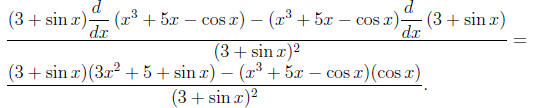
10. Write down a strategy for calculating derivatives .
Solution: See notes online.
| Prev | Next |