Math 201 Exam 2 Review

This is for the night class only.
Work without a calculator. Do not arbitrarily assign values to any unknown
quantity. Always explain your reasoning and show your work.

0. Go over all the homework, quizzes, your notes, and other problems from the book (for
example, to save space, no illustrations are on this review sheet, though the book contains
quite a few problems that require an illustration).

1. Suppose 5 · 3 = 3 (mod n). Find all possibilities for n.

2. Explain how to mentally calculate a tip of 15%.
3. Order the fractions 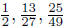from smallest to largest without doing any computations.

4. Use the Euclidean algorithm to find the GCD of 5922 and 10647.

5. For what value(s) of the digit a is the number 7541a6142 divisible by 3 ?

6. Find the prime factorization of 364. How many divisors does it have ?

7. Invent a word problem that requires the calculation of .

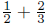8. Suppose the LCM of a and b is 5175 and their GCD is 345. Find their product a · b.

9. Use an area model to explain the computations 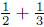and .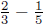

10. Use the car number line model to explain the computations 7 − 3 and 4 + (−5).

11. Find all divisors of .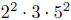

12. Suppose 0 < d < b are integers. Prove that .

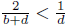13. Use an area model to illustrate the fact that 2/3 is equal to 4/6.

14. Explain why part of the defining formula for |n| has a negative sign in it, despite the
fact that |n| is never negative.

15. How you would use patterns to show students how to find the product of a positive
number times a negative number, and the product of two negative numbers.

16. Explain in words how you would find all primes less than 200.

17. Explain how you would mentally total up the score on an exam which has the following
marks: −3, −9, −6, −2, −7, −8, −4, −5, −2.

18. A student insists that 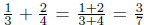. How would you use models to explain the
correct way to add fractions ?

19. Use the mail-time model to explain the computations (−3) · (15) and 6 · (−7).

20. In a 24 hour clock, what numbers can be divided by 5 (with unique solutions) ?

21. Dividing 52611 by 3 is equivalent to what missing factor multiplication problem ?

22. Does the associative rule hold for every arithmetic operation ?

23. Use the charged particle model to explain the computations 5 − 7 and (−2) · (−5).

24. Determine when |n + m| = |n| + |m|.

25. Explain how you would mentally calculate 48 · 120

26. Give two different word problems whose solutions either require a GCD or a LCM.

27. Determine whether or not 7153418254132367123261 is divisible by 9.

28. Using the mail-time model, explain why an inequality A < B of positive numbers is
“flipped” when you multiply by −1.

29. Use the strip model to explain the computations 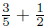and .

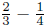30. Use the car number line model to explain the computations 3 × −35 and (−2) × 40.

31. You are substituting for a sick colleague. His notes say “the mailman taking away a
bunch of bills makes you richer which shows” but the rest is smudged. What do you think
the notes were saying ?

32. Without doing any calculations, determine whether or not 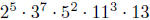divides


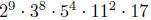
33. You have $40 to spend and you need to buy two gallons of milk at $2.29 a gallon, 1
dozen eggs at $1.63, 2 rolls of paper towels at $1.21 per roll, a 5 lb roast at $1.47 a pound,
2 boxes of cereal at $3.19 each, and an azalea for $9.95. Explain how to mentally estimate
things so as to determine whether or not you can afford all of these items.

34. A student is working on fractions using the area model where a circle of radius 1
represents one unit. The student asserts that thus a circle of radius 1/2 must represent 1/2
units. What would you say to the student ?

35. Give three explanations for why the product of any two negative numbers is positive.

36. Use the number line to solve |2 − x| = 7 for x.

37. Use the area model to explain why there is a fraction between 5/8 and 6/8 .

38. Find any and all solutions to 3x − 6 = 5, (mod 8).

39. Give two examples of real numbers that cannot be written as fractions of integers.

40. Use the charged particle model to explain why −(−4) = 4.

41. Assume 5 divides n. What does the rectangular area model say here ?

42. Explain why it is useful for future teachers to study division in clock arithmetic.

43. Explain why any even length palindrome number is divisible by 11.

44. Use the colored counter model to explain the computation 4 × (−3).

45. Explain the algebraic steps involved in doing the calculation .

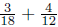46. A bright student uses the formula n² − 81n + 1681 for ten different values of n and
concludes that it always outputs a prime number. What would you say to her ?

47. In order to test the number 221 for primality, we need to try to divide by small primes.
What is the largest prime we need to try ?

48. How can LCM’s be used in the arithmetic of fractions ? Are they necessary ?

49. Explain what the divisibility test for dividing by 4 is. Then explain why it works,
using remainders and the distributive law .

50. Suppose you have the prime factorizations of two numbers. Explain how to find their
GCD and LCM. Why is it better in general to use the Euclidean algorithm ?