Linear Independence and the Wronskian
| Definition: Two functions f and g are said
to be linearly dependent on an interval I if there exist two constants 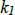 and and
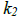 , not both zero, such that , not both zero, such that
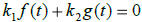 (defining equation) for all t in I.
The (defining equation) for all t in I.
Thefunctions f and g are said to be linearly independent on an interval I if they are not linearly dependent, i.e., if 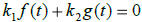 only if only if
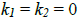 . .Note that f and g are linearly dependent on some interval I if g is a multiple of f . |
To test a set of functions for linear
independence/dependence on I where it is not obvious that one is a
multiple of the other follow these steps: 1) Insert the functions in question
into the defining equation. 2)
Obtain two homogeneous equations using two different values for t (t ∈ I)
or letting the second equation
be the derivative of the first. 3) Take the coefficient determinant of the two
equations. If the
determinant ≠ 0 there is a unique solution, namely,
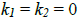 which tells you that the two functions are
which tells you that the two functions are
linearly independent on I. If the determinant = 0 this is inconclusive. In this
case algebraically solve for
the values of the 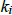 .]
.]
Example 1. Determine whether the following sets of functions are linearly
independent or dependent on
a) f (t) = t , g(t) = 2t
b) f (t) = t +3, g(t) = 2t
c) f(t) = t, g(t) = |t|
| If two functions are solutions of the same linear
homogeneous o.d.e. L[y] = 0, then we have the following theorem: Theorem. Let 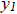 and and
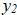 be solutions of L[y] y'' + p(t)y' +
q(t)y = 0 where p and q are continuous be solutions of L[y] y'' + p(t)y' +
q(t)y = 0 where p and q are continuouson I. Then 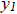 and and
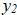 are linearly independent on I if and
only if are linearly independent on I if and
only if 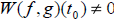 for all t in I. for all t in I.Alternately,  and and
 are linearly dependent on I if and
only if are linearly dependent on I if and
only if 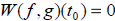 for all t in I. for all t in I. |
Example 2. Suppose the functions
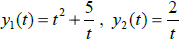 are known to be solutions of the same 2rd-
are known to be solutions of the same 2rd-
order L [y] =0.
a) Use the Wronskian to determine the intervals on which these solutions are
linearly independent.
b) What is the most simplified version of the fundamental set?
Example 3. Use the Wronskian to determine which set
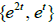 or
or 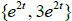 could not be a fundamental
could not be a fundamental
set of a 2nd order L[y] = 0.
| The superposition and proportionality principles
that characterize L[y] = P(t)y'' + Q(t)y' + R(t)y tell us that any multiple of a solution or linear combination of solutions of L[y] = 0 is also a solution of L[y} = 0. |
Example 4. Show that if 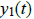 and
and
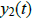 are solutions of L[y] = 0, then so is
are solutions of L[y] = 0, then so is
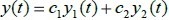 .
.
Example 5. Given that 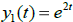 and
and
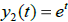 are solutions of the same 2nd order
are solutions of the same 2nd order
L[y] = 0, which functions below are also solutions of this same L[y] = 0?
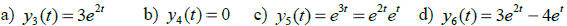
PROPERTIES OF THE FUNDAMENTAL SET OF L[y] = 0
Fundamental sets in "closed form"
As it turns out we are able to find fundamental sets in "closed form" of L[y] =
0 only if L[y] has constant
coefficients or in limited cases where L[y] has variable coefficients .
Otherwise, we have to resort to
series or other methods of representing general solutions of L[y] = 0.
How do we find fundamental sets of homogeneous linear equations L [y] = 0 in
"closed form"?
•
If L[y] has constant coefficients, or if L[y] has a certain pattern of variable
coefficients (Euler equations), the
fundamental set is found by assuming the form of the solutions: In the case of
constant coefficient L[y] the
form is 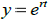 . In the case of Euler equations the form is
. In the case of Euler equations the form is
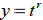 .
.
•
Inserting the form of the solution into L[y] = 0 yields a characteristic
polynomial equation in the case of
constant coefficient L[y] and a similar kind of equation in the Euler case.
•
The roots of these equations determine the functions of the fundamental sets of
L[y] = 0.
•
Note that if L[y] is second order there will be two functions in the fundamental
set. If L[y] is third order there
will be three functions in the fundamental set. Etc.
Equivalent Statements for Solutions of 2nd- Order L[y] = 0
Given the 2nd-Order L[y] = 0, P(t)y'' + Q(t)y' +R(t)y = G(t) , the following
statements are equivalent:
1. The fundamental set 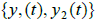 is a set of two solutions of L[y]
= 0 defined on some t-interval I.
is a set of two solutions of L[y]
= 0 defined on some t-interval I.
2. The two solutions of the fundamental set of L[y] = 0 are linearly independent
on I.
3. The Wronskian of the solutions 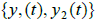 exists and will never
equal zero on I .
exists and will never
equal zero on I .
4. The general solution, 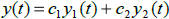 , is a linear
combination of
, is a linear
combination of 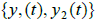 .
.
5. The Existence and Uniqueness Theorem guarantees a unique solution for all
initial conditions with 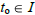 .
.
6. The specific solution of the I.V.P. of L[y] = 0 with
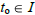 will be defined
throughout the interval I.
will be defined
throughout the interval I.
| Prev | Next |