The Real Zeros of a Polynomial Function
1. The Division Algorithm for Polynomials (p. 363)
If f(x) and g(x) denote polynomial functions and if g(x) is not the zero
polynomial, then there are unique polynomial functions q(x) and r(x)
such that
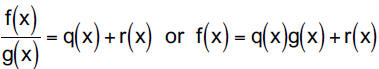
where r(x) is either the zero polynomial or a polynomial of degree less
than that of g(x). The function f(x) is called the dividend, g(x) is the
divisor, q(x) is the quotient and r(x) is the remainder.
Example 1: Find the quotient and remainder, if any.
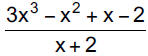
Example 2: Find the quotient and remainder, if any.
(x4 + x2 + 2)÷ (x − 2)
The Remainder Theorem: Let f be a polynomial function. If
f(x) is
divided by (x – c), then the remainder is f(c).
Example 3: Use the Remainder Theorem to find f(3) if
f(x) = 2 x2 − 3x + 2
3. The Factor Theorem (p. 364)
• If f(c) = 0, then x – c is a factor of f(x), and
• If x – c is a factor of f(x), then f(c) = 0.
Example 4: Use the Factor Theorem to determine if x – 2 is
a
factor of f(x) = x3 − 2x2 − 9x + 18.
4. Synthetic Division (pp. 56, 365)
If f(x) is divided by x – c, synthetic division can be used instead of the
long division process. The synthetic division process is fully
described on page fifty-six of your text, however a brief summary is
given below.
To divide a polynomial function f(x) by x – c
1. Write f(x) in descending powers of x. Copy the coefficients in
order , inserting a zero for any missing powers of x.
2. Insert the usual division symbol , placing the ordered numbers
from the step above under the symbol. Outside the symbol
place c.
3. Leave the row under the ordered numbers empty , and place a
line separating this row from the next row down. Bring down the
first coefficient underneath this line.
4. Multiply c by the number you brought down. Place the product
in row 2 underneath the second coefficient.
5. Add the row 2 entry to the entry above it and put the sum under
them in the third row.
6. Continue this process until no more entries are available in row
1.
7. The final entry in row 3 is the remainder. The other entries are
the coefficients of the polynomial, in descending powers, whose
degree is one less than the degree of f(x).
Example 5: Use synthetic division to find the quotient and
remainder.
(x4 − 3x2 − x + 2)÷ (x − 2)
Steps 1 and 2: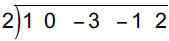
Step 3 :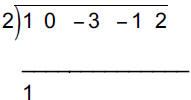
Step 4 and 5 :
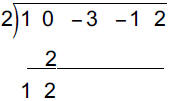
Step 6 :

Step 7: The quotient is x3 + 2x2 + x + 1 and the remainder is 4.
5. The Number of Real Zeros of a Polynomial Function
A polynomial function cannot have more real zeros than its degree.
Example 6: What is the maximum number of real zeros of the
given polynomial?
f(x) = 3x2 − 4x3 + 2x − 7
6. The Rational Zeros Theorem (p. 366)
degree 1 or higher of the form:
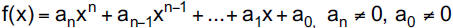
where each coefficient is an integer. If p/q, in lowest terms , is a
rational zero of f, then p must be a factor of a0 and q must be a factor
of an.
Using this theorem, you can list all of the possible rational
zeros of a
polynomial by listing all fractions that have a numerator that is a
factor of a0 and a denominator that is a factor of an.
Example 7: List all of the potential zeros of the polynomial:
f(x) = 2x3 + 3x2 − x + 6
7. Finding the Real Zeros of a Polynomial Function (p. 368)
Steps for Finding the Real Zeros of a Polynomial Function
Step1: Use the degree of the polynomial to determine the maximum
number of real zeros.
Step 2: (a) If the polynomial has integer coefficients, use the Rational
Zeros Theorem to identify those rational numbers that
potentially can be zeros.
(b) Use substitution , synthetic division or long division to test
each potential rational zero.
(c) Each time that a zero (and thus a factor) is found, repeat
Step 3 on the depressed equation.
Step 3: In attempting to find the zeros, remember to use (if possible)
the factoring techniques that you already know.
Example 8 (p.375, #56): Solve the polynomial equation (Find
the zeros of the polynomial function)
4x5 + 12x4 − x − 3 = 0
8. Approximating the Zeros of a Polynomial Function by Using a
Graphing Calculator
To use a graphing calculator to approximate the zeros of a
polynomial function, enter the function into the “y=” blank. Graph the
function. Press 2nd Calc and choose “zeros” from the menu.
Following the instructions on the screen, move the cursor on the
graph to the left side of the zero (a left bound), then press “enter”.
Move the cursor to the right side of the same zero (a right bound),
then press “enter”. Move the cursor as close to the zero as possible,
then press enter again. The calculator will return an approximate
value for the zero .
Example 9: Use a graphing calculator to approximate, to two
decimal places , the zeros of the given polynomial.
f(x) = 3x3 −10x + 9
Section 4.6 Answers
Example 1: q(x) = 3x2 − 7x + 15, r(x) = −32
E xample 2 : q(x) = x3 + 2x2 + 5x + 10, r(x) = 22
Example 3 : (2x2 − 3x + 2)÷ (x − 3), q(x) = 2x + 3, r(x) = 11
so f(3) = 11
Example 4 : f(2) = 23 − 2•22 − 9•2 + 18 = 0
so f(2) = 0 and (x − 2) is a factor of f
Example 5: x3 + 2x2 + x + 1 remainder 4.
Example 6: The maximum number of real zeros is three.
Example 7 :
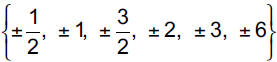
Example 8 :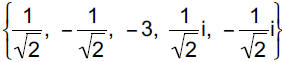
Example 9:
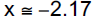
| Prev | Next |