Graphs and Functions
3.3 Linear Functions
3.3.1 Graph Linear Functions
A linear function is a function of the form
f(x) = ax + b
The graph of a linear function is a straight line. Also, for linear
functions, the domain is the set of
all real numbers R . Recall: When graphing y = f(x).
3.3.2 Intercepts and Standard Form
The standard form of a linear equation is
ax + by = c
where a, b, and c are real numbers and a and b are not both 0.
In this form it is frequently easier to graph the equation using the intercepts.
The x-intercept
is the point where the graph crosses the x-axis. The y-intercept is the point
where the graph
crosses the y-axis.
•To find the y-intercept, set x = 0 and solve for y .
•To find the x-intercept, set y = 0 and solve for x.
EX 12. 1. Graph 3x = 6y + 12 using the x- and y-intercepts.
2. Graph f(x) = 1/2x + 2 using the x- and y-intercepts.

3. Graph -2x + y = 0

3.3.3 Vertical and Horizontal Lines
Horizontal Lines
Any equation of the form y = b will always be a horizontal line.
EX 13. Graph the equation y = 4 (or written f(x) = 4)

Vertical Lines
Any equation of the form x = a will always be a vertical line.
EX 14. Graph the equation x = 4

3.3.4 An Application
EX 15. Suppose a store owner sells widgets for $30 each. If her monthly
expenses are $3,000,
answer the following:
1. Construct a function that relates the number of widgets sold to the pro
fits.
2. How many widgets must she sell to break even?
3. Graph the profit function.

3.4 Slope-Intercept Form of a Linear Equation
Our goal in this section will be to completely describe a line using two
numbers which reveal certain
characteristics of the line. The characteristics we will use are the y-intercept
and the slope.
3.4.1 Understand Translations
Consider the graph of the function y = 1/2x. What happens if we add 2 to the
right hand side? How
about if I subract 2? Let's graph the following functions on the same coordinate
system .
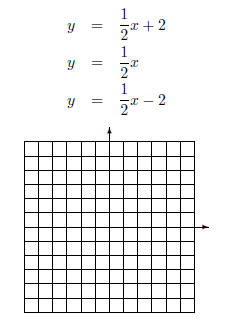
What are the y-intercepts? Each line is parallel to the other, but the new
lines are shifted, or
translated, up or down by two.
3.4.2 Slope
As was mentioned we wish to describe lines using two numerical
characteristics . One of those is the
slope.
Definition 6. The slope of a line is the ration of the vertical change
(or rise) to the horizontal
change (or run).
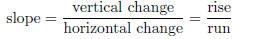
EX 16. We examine how to find slope:
1. Look at the graphs from the previous example , find the slope of the lines .
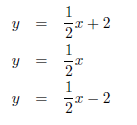
2. Graph the equations y = 2x and and y = 2/3x and find their slopes.

The slope of the line through the distinct points (x1, y1) and (x2, y2) is
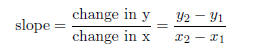
provided that
 We usually use the lowercase letter m to denote the slope.
We usually use the lowercase letter m to denote the slope.
EX 17. Calculate the slope for the following lines:
REMARK 3. From the example we notice the following:
•Lines with positive slope increase as we go from left to right.
•Lines with negative slope decrease as we go from left to right.
•Any horizontal line has zero slope .
•What would the slope of a vertical line be?
3.4.3 Slope-Intercept Form
The slope-intercept form of a linear equation is
y = mx + b
where m is the slope of the line and (0, b) is the y-intercept of the line.
To write an equation in slope-intercept form, solve the equation for y.
EX 18. -
1. Consider the equation y = 2/3x + 2 and determine the slope and y-intercept.
2. Write the equation -3x + 4y = 8 in slope-intercept form and determine the
slope and y-
intercept.
3.4.4 Graphing Linear Equations Using Slope and y-Intercept
EX 19. Graph the following equations using the slope and y-intercept:
| Prev | Next |