Algebra Exam Solutions
1.
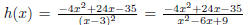The numerator doesn 't factor, so sim-
plify by polynomial division . This is also the best way to determine how h(x)
is a transformation of 1/x2 So when you perform polynomial division, one gets a
quotient Q(x) = -4 and a remainder R = +1. Thus we can write the original
poly as
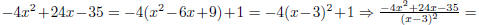
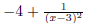Therefore
to get h(x), shift 1/x2 to the right 3 units and down 4
units. (5 pt)
The horizontal asymptote is
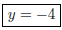since the degree of the numerator is equal
to the degree of the denominator . The vertical asymptote is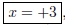
since the
denominator is zero at this point, but the numerator is non-zero. (3 pt)
(2
pt)
2. From the statement of the problem, we must assume that
the relationship
between dress sizes is linear . So, I expect a linear equation : y = mx + b. Use
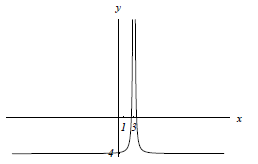
two points on the graph given in the problem statement: (4, 32), (12, 48).
A) So,
.
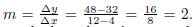Then, as usual, use another point on the
graph to calculate the y -intercept b. So, y = 2x + b => 32 = 2(4) + b => 32 =
8 + b => b = 24. Hence,
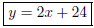. (3 pt)
B) f(x) = 2x + 24, so f(6) = 2(6) + 24 = 36, f(8) = 2(8) +
24 = 40, and
f(10) = 2(10) + 24 = 44. (3 pt)
C) Clearly, f(x) = 2x+24 is a line. Thus, the graph passe
the vertical-line test
and is 1 - 1. So, f must have an inverse. So, f(x) = 2x + 24 => y = 2x + 24 =>
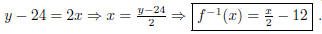(3 pt)
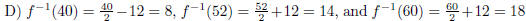(3 pt)
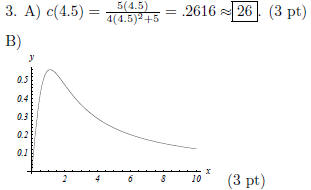
C)Horizontal asymptote: y = 0 (x-axis). This tells you
that the amount of drug
is never negative . The whole graph starts at zero , increases rapidly right after
it is ingested, then slowly filters out of a person' s system . (3 pt)
D) By the graph, the percentage is highest at t = 1.12
hrs. This corresponds to
c(1.12) = .5590 ≈ 56% of drug in a person's bloodstream. (3 pt)
4. If there were real numbers k for which (x - k) is a
factor of the polyno -
mial given, then the remainder upon polynomial division would be zero. In
other words, k is a root or zero of the polynomial. So, one must have that
k4 + 3k2 + 1 = 0, but there are no real numbers that satisfy this equation. (8
pt)
5.
= x4 + 3x3 - 24x2 - 28x + 48
A)x = -2 is a root, since
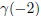= (-2)4 +3(-2)3 -24(-2)2 -28(-2)+48 = 0
(2 pt)
. B) By Synthetic division (with -6 as divisor), one finds that the remainder is
zero. So, yes (x + 6) is a factor of
.
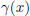(32 pt)
C) In order to do this, one could graph the original polynomial and look for all
places the graph crosses the x-axis. Also, by successive use of synthetic
division:
By (B), (x + 6) is a factor so
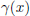= (x + 6)(x3 - 3x2 - 6x + 8). We also know
from (A) that -2 is a root, so that means (x + 2) is another factor. So, divide
(x3 + 3x2 - 6x + 8) by (x + 2) to get the quotient polynomial...by synthetic
di-
vision, you should find that the remainder is zero. Also, that the quotient poly
Q(x) = x2-5x+4. Hence,
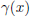= (x+6)(x+2)(x2-5x+4). Now one can easily
factor this remaining Q(x). Therefore,
.
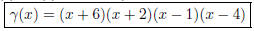(4 pt)
BONUS:
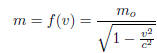
where mo and c are constants so, solve for v .
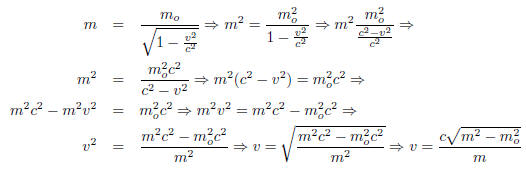
Thus, the inverse is...
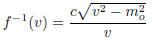
The inverse function f-1(v) gives the velocity corresponding to a given rela-
tivistic mass m.
| Prev | Next |