The Quadratic Equation
Need To Know
▪ Review the quadratic equation
▪ The Principle of Square Roots
▪ Completing the Square
The Principle of Square Roots
The Principle of Square Roots
For all positive real numbers b ,
Reminder: ±
If X2 = k, then
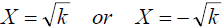
In Words
We use the square root to remove “squared stuff”.
Always remember there are two answers ,
so use the +.
Solve:
9x2 + 16 = 0
(3a – 12)2 = 18
Completing the Square
Figure out what constant term to add to make the
polynomial factor into a perfect square.
x2 + 4x + ____ = ( )2
x2 – 10x + ____ = ( )2
x2 – 24x + ____ = ( )2
x2 + 3x + ____ = ( )2
x2 + bx + ____ = ( )2
Solve by completing the square:
3y2 + 12y + 6 = 0
How to Solve by
Completing the Square
1 If a is not 1 divide
by a on both sides.
2. Put equation in
x 2 + bx = c form.
3. Add the complete
square number to
both sides.
4. Solve the equation
by the square root
method
Solve by completing the square:
2x2 – 2x + 1 = 0
How to Solve by
Completing the Square
1 If a is not 1 divide
by a on both sides.
2. Put equation in
ax2 + bx = c form.
3. Add the complete
square number to
both sides.
4. Solve the equation
by the square root
method
8.1 Conclusion
Ways to Solve Quadratic Equations
1. Factoring method
(Set up: equation must equal zero )
2. Square root method
(Set up: “squared stuff” by itself)
3. Completing the square method
(Set up: the leading coefficient = 1)
| Rating | Doable |
| Easy | Not always |
| Easy | Not always |
end
8.2 The Quadratic Formula
Need To Know
▪ The parts of the quadratic equation
▪ The Quadratic Formula and how to use it
The Quadratic Equation

Example: Find the coefficients.
3x2 - 7x + 11 = 0
For ax2 + bx + c = 0,
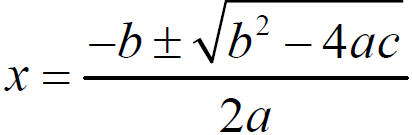
Solve:
y2 + 13 = 6y
How To Solve
1. Put equation in
standard form
(it must equal 0).
2. Find a, b, c
3. Plug into the
formula & simplify
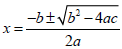
Solve:
x2 – 4x + 4 = 5
How To Solve
1. Put equation in
standard form
(it must equal 0).
2. Find a, b, c
3. Plug into the
formula & simplify
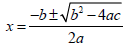
Solve:
r2 = -3r + 8
How To Solve
1. Put equation in
standard form
(it must equal 0).
2. Find a, b, c
3. Plug into the
formula & simplify
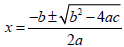
8.2 Conclusion
Ways to Solve Quadratic Equations
1. Factoring method
(Set up: equation must = 0)
2. Square root method
(Set up: “squared stuff” by itself)
3. Completing the square method
(Set up: the leading coefficient = 1)
4. Quadratic Formula
(Set up: equation must = 0)
| Rating | Doable |
| Easy | Not always |
| Easy | Not always |
| Hard | Always |
end
8.3 Applications with Quadratics
Need To Know
▪ Review methods of solving quadratics
▪ Applications
▪ Solving quadratic formulas
8.3 Methods to Solve Quadratics
Ways to Solve Quadratic Equations
1. Factoring method
(Set up: equation must = 0)
2. Square root method
(Set up: “squared stuff” by itself)
3. Completing the square method
(Set up: the leading coefficient = 1)
4. Quadratic Formula
(Set up: equation must = 0)
| Rating | Doable |
| Easy | Not always |
| Easy | Not always |
| Hardest | Always |
| Hard | Always |
Word Problems
Peter’s car travels 200 miles averaging a certain speed.
If the car had gone 10 mph faster, the trip would have
taken 1 hour less. Find Peter’s average speed
During the first part of the trip, Mita’s car traveled 120
miles at a certain speed. Mita then drove another 100
miles at a speed that was 10 mph slower.
Her total trip took 4 hours. What were her speeds?
end
| Prev | Next |