Systems of Linear Equations in Two Variables
Systems of Linear Equations and
Their Solutions
We have seen that all equations in the form Ax + By = C
are straight lines
when graphed . Two such equations, such as those listed above, are called a
system of linear equations . A solution to a system of linear equations is an
ordered pair that satisfies all equations in the system. For example, (3, 4)
satisfies the system
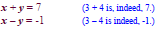
Thus, (3, 4) satisfies both equations and is a solution of
the system. The
solution can be described by saying that x = 3 and y = 4. The solution can also
be described using set notation. The solution set to the system is {(3, 4)} -
that
is, the set consisting of the ordered pair (3, 4).
Text Example
Determine whether (4, -1) is a solution of the system
x + 2y = 2
x – 2y = 6.
Solution Because 4 is the x-coordinate and -1 is
the y-coordinate of (4, -1),
we replace x by 4 and y by -1.
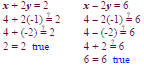
The pair (4, -1) satisfies both equations: It makes each
equation true. Thus, the
pair is a solution of the system. The solution set to the system is {(4, -1)}.
Solving Linear Systems by Substitution
• Solve either of the equations for one variable in
terms of the other. (If one of the equations is
already in this form, you can skip this step.)
• Substitute the expression found in step 1 into the
other equation. This will result in an equation in
one variable.
• Solve the equation obtained in step 2.
• Back-substitute the value found in step 3 into the
equation from step 1. Simplify and find the value
of the remaining variable.
• Check the proposed solution in both of the
system's given equations.
Text Example
Solve by the substitution method:
5x – 4y = 9
x – 2y = -3.
Solution
Step 1 Solve either of the equations for one variable in terms of the other.
We begin by isolating one of the variables in either of the equations. By
solving for x in the second equation, which has a coefficient of 1, we can avoid
fractions.
x - 2y = -3 This is the second equation in the given
system.
x = 2y - 3 Solve for x by adding 2y to both sides.
Step 2 Substitute the expression from step 1 into
the other equation. We
substitute 2y - 3 for x in the first equation.

Solve by the substitution method:
5x – 4y = 9
x – 2y = -3.
Solution
This gives us an equation in one variable, namely
5(2y - 3) - 4y = 9.
The variable x has been eliminated.
Step 3 Solve the resulting equation containing one variable.
| 5(2y – 3) – 4y = 9 | This is the equation containing one variable. |
| 10y – 15 – 4y = 9 | Apply the distributive property . |
| 6y – 15 = 9 | Combine like terms . |
| 6y = 24 | Add 15 to both sides. |
| y = 4 | Divide both sides by 6. |
Solve by the substitution method:
5x – 4y = 9
x – 2y = -3.
Solution
Step 4 Back-substitute the obtained value into the equation from step 1.
Now that we have the y-coordinate of the solution, we back-substitute 4 for y
in the equation x = 2y – 3.
| x = 2y – 3 | Use the equation obtained in step 1. |
| x = 2 (4) – 3 | Substitute 4 for y. |
| x = 8 – 3 | Multiply. |
| x = 5 | Subtract . |
With x = 5 and y = 4, the proposed solution is (5, 4).
Step 5 Check. Take a moment to show that (5, 4)
satisfies both given
equations. The solution set is {(5, 4)}.
Solving Linear Systems by Addition
• If necessary, rewrite both equations in the form Ax +
By = C.
• If necessary, multiply either equation or both
equations by appropriate nonzero numbers so that
the sum of the x - coefficients or the sum of the ycoefficients
is 0.
• Add the equations in step 2. The sum is an equation in
one variable.
• Solve the equation from step 3.
• Back- substitute the value obtained in step 4 into
either
of the given equations and solve for the other variable.
• Check the solution in both of the original equations.
Text Example
Solve by the addition method:
2x = 7y - 17
5y = 17 - 3x.
Solution
Step 1 Rewrite both equations in the form Ax + By = C. We first arrange
the system so that variable terms appear on the left and constants appear on
the right. We obtain
2x - 7y = -17
3x + 5y = 17
Step 2 If necessary, multiply either equation or
both equations by
appropriate numbers so that the sum of the x-coefficients or the sum of
the y-coefficients is 0. We can eliminate x or y. Let's eliminate x by
multiplying the first equation by 3 and the second equation by -2.
Solution
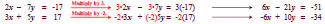
Steps 3 and 4 Add the equations and solve for the
remaining variable.
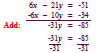 Divide both sides by -31.
Divide both sides by -31.
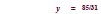 Simplify.
Simplify.
Step 5 Back-substitute and find the value for
the other variable. Backsubstitution
of 85/31 for y into either of the given equations results in
cumbersome arithmetic . Instead, let's use the addition method on the given
system in the form Ax + By = C to find the value for x. Thus, we eliminate y
by multiplying the first equation by 5 and the second equation by 7.
Solution
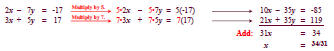
Step 6 Check. For this system, a calculator is
helpful in showing the
solution (34/31, 85/31) satisfies both equations. Consequently, the solution set
is {(34/31, 85/31)}.
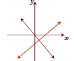
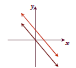
The Number of Solutions to a
System of Two Linear Equations
| The number of solutions to a system of two linear
equations in two variables is given by one of the following.
|
 |
 |
 |
| Exactly one solution | No Solution (parallel lines) | Infinitely many solutions (lines coincide) |
Example

Solution:
2 (2x + 3y = 4) multiply the first equation by 2
-4x - 6y = -1
4x + 6y = 8
-4x - 6y = -1
0 = 7 Add the two equations
No solution
Systems of Linear
Equations in Two
Variables
| Prev | Next |