Solving Quadratic Inequalities

Example: Solve 3x² + 3x - 6 < 0

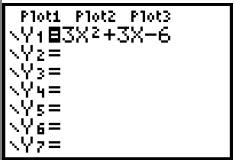	Step 1: Go to and under Y1 enter 3x² + 3x - 6. Press . You are graphing a quadratic function , so the graph should be a parabola .
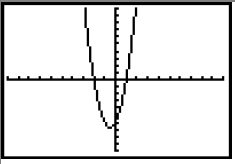	Step 2: You want to determine where the quadratic function is less than 0. So you need to look at the graph and determine what part of the graph lies below the x-axis or the line y = 0.
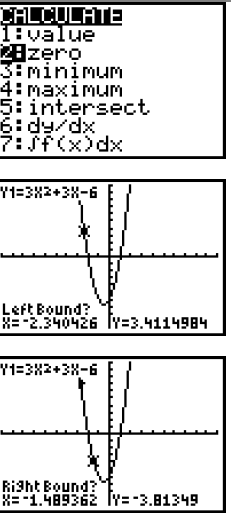	Step 3: The part of the graph that is below the x-axis is the part that lies between the x-intercepts. To find these x- intercepts or zeroes , go to , the CALCULATE menu, and select 2: zero . Press . To find the intercept on the left , use the arrow keys to move the cursor to the left of the point, press . Then move the cursor to the right of the point, press , and then press again. The x-intercept is x= -2.
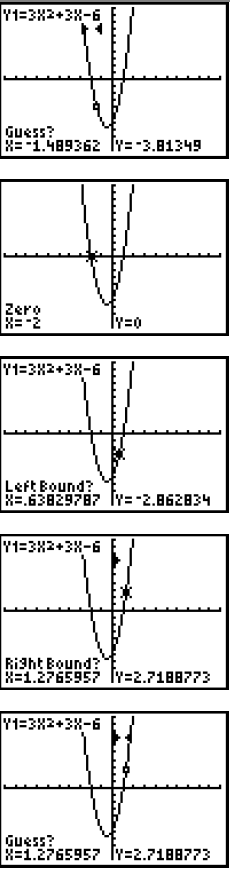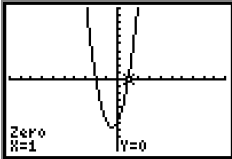	To find the intercept on the right, go to , the CALCULATE menu, and select 2: zero . Press . Then repeat the process used above. The other intercept is x = 1.
	Step 4: Remember - since you are solving an inequality , the solution will be an interval or the union of two intervals. The solution to this inequality is the interval (-2, 1) or -2 < x < 1.
	Step 5: If you want to determine where a quadratic is greater than 0, you need to look at the graph and determine what part of the graph lies above the x-axis.