Polynomials and Factoring
Sec. 7.6- Polynomials and Factoring -Day 2
HW #5, 18, 19, 39*, 43*, 45*, 46, [47-99 e.o.o.], 100
* Also use the CFQ and Tic-Tac-Toe Methods on these
* Return quizzes & discuss.
* Finish up Sec. 7.6 on Polynomials and Factoring
Looking ahead: Next quiz will be Tuesday 11/11.
Factoring Polynomials : A few special cases.
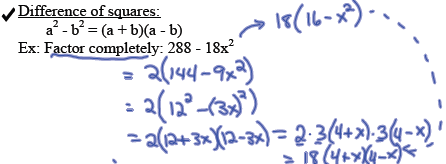
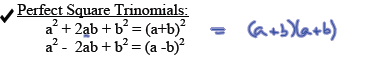
Example: Fill in the blank in the polynomial below so
that it is a perfect square trinomial . Then factor it
completely.
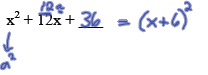
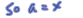
Factoring Polynomials: A few special cases.
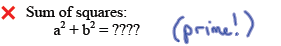
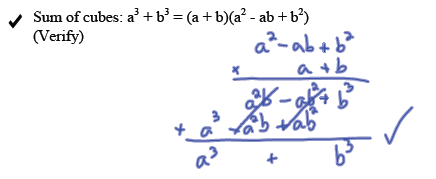
 Difference of cubes :
Difference of cubes :
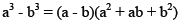
Factor completely:
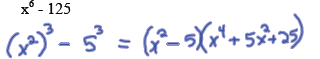
More complex cases : when the lead coefficient is not 1.
Factor the following trinomials:
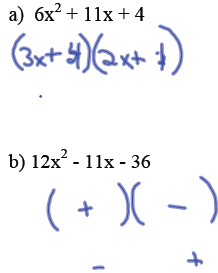

Other Methods of Factoring:
1. Common Factor Quotient (CFQ) Method
2. Tic-Tac-Toe Method
First, we'll illustrate the CFQ method of factoring.
(Full description on next slide).
Factor the following trinomial using the CFQ Method:
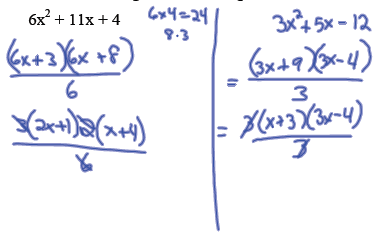
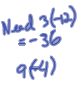
Using the Common Factor Quotient (CFQ) Method of Factoring:
To factor ax^2 + bx + c:
1. The first step is to set up the following:
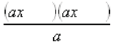
2. Find two factors of ac that have a sum of b .
That is find e and f so that ef = ac, and e + f = b.
3. Place e and f as shown:
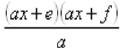
4. Check to see if there is anything that can be factored
out of the
parentheses in each of the 2 sets .
5. Reduce the fraction , if possible.
Example: Factor 24x^2 + 25x + 6.
Next, let's illustrate the Tic-Tac-Toe Method.
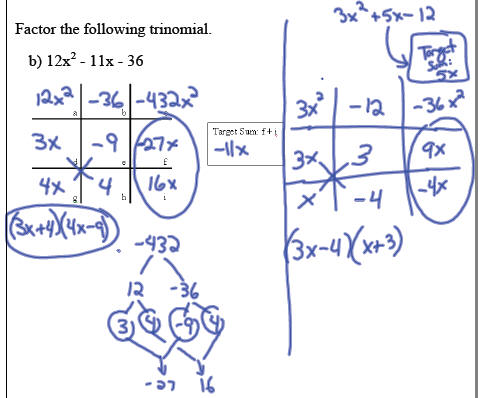
Using the Tic-Tac-Toe Method of Factoring
Example: Factor 24x^2 + 25x + 6 (same example as CFQ).
1. Put the first term of the trinomial in cell a
2. Put the last term of the trinomial in cell b
3. Cell c is equal to the product of cell a times cell b (first term times last
term)
4. The target sum is equal to the middle term.
5. The next step is the key cells, f and i. Cell f times cell i should equal
cell c
and add to the target sum. At this point cell f and i are interchangeable
6. Cell d is the greatest common factor of cell a and cell f.
7. The rest of the cells can be filled in by finding the missing factor (cell d
times
cell e results in cell f; cell d times cell g results in cell a, …)
8. The factors of the trinomial are on the diagonals of cells
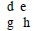
More practice: Factor completely.
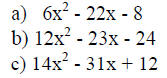
| Prev | Next |