PREALGEBRA FINAL EXAM REVIEW
NOTE: On the MAT 0012 final exam you will be asked
to complete the first half of the
exam without a calculator and the second half with a calculator. Therefore, when
completing this review packet, you should complete the first part without a
calculator and
the second part with a calculator.
NON-CALCULATOR PORTION
Directions: Show all supporting work. Always attach
the correct units where possible.
Reduce all fractions to lowest terms .
Section 1.2
1) Write 42,097,823 in word form
2) Write the following whole number
in standard form:
Nine hundred eighty thousand,
six hundred seventeen
Section 1.3
3) Add: 25,735+1,946+349+87
4) Subtract: 76,437-8,978
Section 1.4
5) Round 43,874 to the nearest
thousand
6) Round 231,568,672 to the nearest
million
Section 1.5
7) Multiply: 3,748× 43
8) Find the area of a rectangular
garden with a length of 42 feet
and width of 37 feet.
Section 1.6
9) Divide: 5684 ÷14
10) Divide: 73,753 ÷801
Section 1.7
11) 42 (9 − 7) + (5 − 2)3
12) 102 ÷ 5× 2 −15
Section 1.8
13) Evaluate
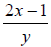
when x = 5 and y = 3
14) Evaluate 3x + 7xy when x = 2
and y = 4
Section 2.1
For numbers 14 and 15, Insert >, < or =
between each pair of numbers to make a
true statement.
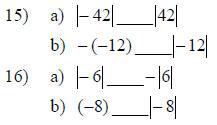
Section 2.2
17) − 5 + 24 + (−7)
18) − 8 + (−23) +17 + (−7)
Section 2.3
19) − 2 − (−12) + 3 − 7
20) 8 + (−5) − 4 − (−14)
Section 2.4
21) −12(−35)
22) −360 ÷ 6
Section 2.5
23) Simplify: (7 −11)2 ÷ (2 − 4)2
24) Evaluate x2 + 3x −1 when
x = −2
Section 2.6
25) Solve and check your solution :
y + 7 = 2
26) Solve and check your solution:
− 9x = 81
Section 3.1
27) Simplify the following by
combining like terms :
3x − (5x + 3) + 4
28) Simplify the following by
combining like terms:
− (5x + 3) − 2(x − 5) +13
Section 3.2
29) Solve for x :
5x + 30 − 4x − 28 = 10
30) Solve for x :
12x +10 = 11(x −1)
Section 3.3
31) Solve for x : 5x +1 = 2(3x − 5)
32) Solve for x :
2 − 3(5x + 2) = 2(3 − 5x)
Section 3.4
33) Translate into an algebraic
equation and solve. Use x to
represent “a number.”
Three times the sum of a number
and five is the same as the sum
of that number and one.
Section 4.1
34) In a pre -algebra class containing
25 students, there are 14 women.
a) What fraction of the class
is female?
b) What fraction of the class
is male?
Section 4.2
35) Simplify the fraction:
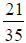
36) Find the prime factorization of
540. Write in exponential form .
Section 4.3
37) Multiply. Write the product in
simplest form.
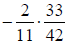
38) Divide. Write the quotient in
simplest form.
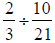
Section 4.4
39) Add and simplify :
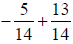
Section 4.5
40) Add:
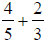
41) Subtract: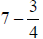
Section 4.6
42) Use the order of operations to
simplify the following
expression:
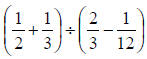
Section 4.7
43) Add and express the answer as a
mixed number in simplest form:
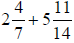
44) Subtract and express the answer
as a mixed number in simplest
form:
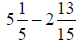
Section 4.8
45) Solve the following equation and
simplify:
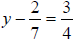
46) Solve the following equation and
simplify:
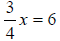
Section 5.1
47)Write 4.65 in word form.
48) Round 3.2791 to the nearest
hundredth
Section 5.2
49) Perform the indicated operations:
− 8.01+ (−9.7) −12.082
Section 5.3
50)Multiply: (23.45) · (3.5)
Section 5.4
51) Divide using long division:
188.6 ÷ 2.3
Section 5.5
52) Simplify the following
expression: (5.1− 4.3)2 + (.5)2
Section 5.6
53) Solve the following equation:
.3x − 7.1 = 80.8
Section 5.7
54) Find Jill’s average (mean) test
grade if her grades are: 79, 83,
92, 68 and 87. Round the
average grade to the nearest
whole number.
Section 6.1
55) There are 2 black pens and 10
orange pens in a jar.
a) What fraction of the pens
is orange?
b) Write the ratio of black
pens to orange pens.
56) The ratio of males to females at
Jones High School is 5:4. If there
are 800 females that attend
Jones, how many males attend?
Section 6.2
57) Solve the proportion for the
given variable .
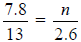
Section 6.3
58) Find how far apart Albany and
Rochester are in Kilometers if
their corresponding points on a
map are 15 centimeters apart.
Use 1 centimeter = 30
Kilometers.
Section 6.4
59) Evaluate
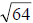
60) Evaluate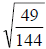
Section 7.1
61)Write 1.4% as a decimal
62) Write 8.32 as a percent
Section 7.2
63) Solve: What is 20% of 60?
64) Solve: 46 is what percent of 50?
Section 7.3
65) Set up a proportion and solve:
What percent of 500 is 125?
Section 7.4
66) From 2005 to 2008, the value of
a house decreased from $270,000
to $195,000. Find the percent
decrease of the price of the
house. Round answer to the
nearest tenth of a percent.
Section 7.5
67) A $350.00 suit is on sale for 20%
off.
a) Find the amount of
discount
b) Find the sale price
Section 7.6
68) Victor borrowed $1,000 at 6%
simple interest. How much
money will Victor owe after one
year.
Section 9.2
69) Find the perimeter of the
geometric figure below:
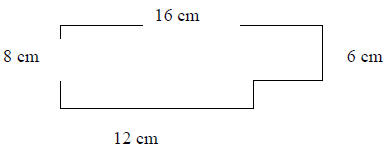
Section 9.3
70) Which of the following has a
greater area?
a) A square with one side
measuring 13 inches
b) A circle with a diameter
of 14 inches?
CALCULATOR PORTION
Directions: Calculators may be used on the
following problems. However, in order to
receive any partial credit on the final exam, you should show all work and state
how you
are getting your answers. On the final exam, incorrect answers without showing
work
will receive no credit. Always attach the correct units where possible. Reduce
all
fractions to lowest terms.
Section 1.3
70) Bob can’t decide whether to buy a
used Buick or a used Ford. The
Buick costs $3,570 while the Ford
costs $2,750. How much less
expensive is the Ford?
71) What is the perimeter of a
rectangular lawn that measures 22
meters by 9 meters?
Section 1.4
72) For a full-time student, the average
cost for a semester of classes at
MCC is $936.28. Books cost
$419.17 and miscellaneous supplies
cost $287.58. Round the total
amount for the semester to the
nearest dollar.
Section 1.5
73) Find the area of the geometric figure
below:
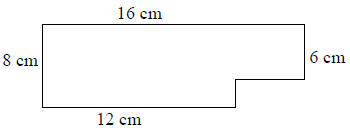
74) Billy’s car gets 12 miles per gallon
of gasoline. How many miles can
Billy drive on 7 gallons of gasoline?
Section 1.6
75) Eddie needs to paint a fence which
has 10,080 square feet of surface.
One gallon of paint covers 576
square feet. How many whole
gallons of paint will he need?
Section 1.7
76) Perform the indicated operations:
12 + (6 ÷ 3)2 ·3 − 2
77) Perform the indicated operations:
12 − 8 ÷ 4 · (5 − 3)2
Section 1.8
78) Translate into an algebraic
Expression. Let x represent
“a number.”
The quotient of twice a number
and thirteen.
Section 2.1
79) Simplify:
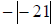
| Prev | Next |