Factoring Polynomials
Types of Factoring
1) Factor by taking out a Greatest Common Factor (GFC)
2) Factor a trinomial as two binomials .
3) Factor a binomial as a difference of two squares
4) Factor a binomial as a difference of cubes or a sum of cubes
Factoring out a Greatest Common Factor
Taking out a greatest common factor is essentially the same as working the
distributive
property backwards .
Review of distributive property
3(x + 5) = 3x + 3·5 = 3x +15
Example 1
Factor out a greatest common factor 4x +16
Solution : 4x +16 = 4(x + 4)
Example 2
Factor out a greatest common factor 5x − 35
Solution: 5x − 35 = 5(x − 7)
Example 3
Factor out a greatest common factor
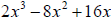
Solution:
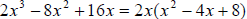
Example 4
Factor out a greatest common factor
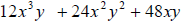
Solution:
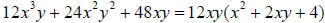
Factoring a trinomial as two binomials
Factoring a trinomial is the same as working the FOIL process
So, here is a short review of FOIL
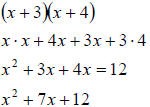
Example of factoring a trinomial as two binomials
Factor x2 +10x + 25
In this example you want to find two numbers that multiply to get 25 and add to
get 10.
By using x as the first entry in each binomial you get:
x2 +10x + 25 = (x + 5)(x + 5)
Here are some similar examples
Example 5
Factor x2 −10x + 24
Answer: (x − 6)(x − 4) Hint: Find two numbers that multiply to get 24 and add to
get -
10
Example 6
Factor x2 − 2x − 35
Answer: (x − 7)(x + 5) Hint: Find two integers that multiply two get -35 and add
to get -2 which is the factors -7 and 5
Example 7
Factor x2 + 4x −12
Answer: (x − 2)(x + 6)
Example 8
Factor 3x2 + 7x + 2
Answer: (3x +1)(x + 2)
Factor a binomial as a difference of squares
Factor x2 − 4
Answer: (x − 2)(x + 2) Hint: Basically use the FOIL process backwards again and
find two integers that multiply to get -4 and add to get zero . This process will
cancel out
the x- terms .
Check:
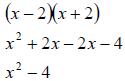
Other similar examples
Example 9
Factor m2 − 36
Answer: (x − 6)(x + 6)
Example 10
Factor x2 −144
Answer: (x +12)(x −12)
Example 11
Factor 9x2 − 25y2
Answer:
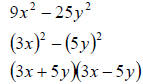
General Form of a Difference of Squares: A2 − B2 = (A + B)(A − B)
Difference of Cubes and sum of Cubes
Main formulas
Difference of Two Cubes
A3 − B3 = (A − B)(A2 + AB + B2 )
Sum of Two Cubes
A3 + B3 = (A + B)(A2 − AB + B2 )
Example 12
Factor x3 − 27
Answer:
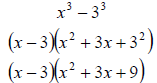
Example 13
Factor x3 + 64
Answer:
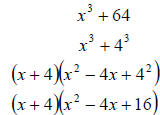
Example 14
Factor x3 + 8
Answer;
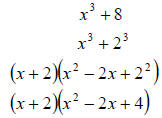
Example 15
Factor 8x3 − 27y3
Answer;
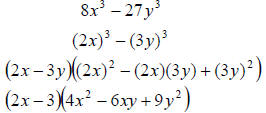
| Prev | Next |