Number Systems

We begin by assuming there is a set R of real numbers that are characterized by a set of axioms
listed below. [To see how the integers, rationals and real number system can be generated from
the axioms of set theory, see e.g. Basic Set Theory by Azriel Levy. Rudin (Chap. 1) demonstrates
one method for constructing the set of real numbers from the set of rational numbers.]

The Axioms of R

These axioms are presented and discussed in Royden (Chap 2) and Rosenlicht (Chap 2). The
discussion of the field and order axioms below largely follows Rosenlicht.

(A) Field Axioms

The operations ‘+’ and ‘٠’ define a field on R. That is, for any x, y, z ∈ R:
i. x + y = y + x and x ٠ y = y ٠ x (addition and multiplication are commutative )
ii. (x + y)+z = x+(y + z) and (x ٠ y) ٠z = x ٠(y ٠ z) (addition and multipliation are associative)
iii. (x + y) ٠ z = x ٠ z + y ٠ z ( distributive law )
iv. x + 0 = x and x ٠ 1 = x, where 1 ≠ 0 (existence of identity elements for addition and
muliplication)
v. x+(-x) = 0 and (x ٠x^-1 = 1 if x ≠ 0). (existence of an additive and multiplicative inverses)

We define x - y ≡ x + ( -y ) and 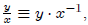and xy = x ٠ y.

• Many different fields satisfy these axioms. If we define 1 + 1 = 0. Then {0, 1} is a field. What
is -1 in this case?

• The rational and complex number systems are fields. The system of integers is not a field. Why
not?

The field axioms imply the standard rules of arithmetic that involve just addition, multiplication
and equality, some of which are listed below. Proofs are provided in the Appendix.

• 0, 1, -x, and x^-1 are uniquely defined.

• - (-x) = x and (x^-1) ^-1 = x.

• (a) 0x = 0 and (b) xy = 0 and x ≠ 0 imply y = 0.

• - (x + y) = -x - y and (xy)^-1 = x^-1y^-1

• - (xy) = (-x) y

• (-1) x = -x

• (-x)(-y) = xy

(B) Order Axioms

To derive the rules of arithmetic that involve inequalities, we require the additional order axioms.
There is a subset 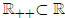such that
i. x, y ∈ R₊₊ implies x + y ∈ R₊₊ and xy ∈ R₊₊.
ii. x ∈ R₊₊ implies -x 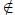R₊₊
iii. If x ≠ 0, then either x ∈ R₊₊ or -x ∈ R₊₊.

If x ∈ R₊₊, we say that x is a positive number. If -x ∈ R₊₊, we say that x is a negative number.
We call R₊ ≡ R₊₊ ∪ {0} the set of nonnegative numbers and R _- ≡ R\R₊₊ the set of nonpositive
numbers. (Observe that B(ii) implies 0 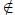R₊₊ since -0 = 0.)

A field that satisfies the order axioms is called an ordered field. We define the relation (R, ≥) by
x ≥ y if and only if x - y ∈ R₊₊ ∪ {0} .

• (R, ≥) is a linear order .
٠ (R, ≥) is transitive since (i) implies that if x -y ∈ R₊ and y -z ∈ R₊ then (x - y)+(y - z) =
x - z ∈ R₊.
٠ (R, ≥) is reflexive since x - x = 0 ∈ implies R₊.
٠ (R, ≥) is antisymmetric since (iii) implies x - y ≠ 0 implies x - y ∈ R₊, which implies that
y - x 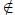R₊.
٠ (R, ≥) is complete since (ii) implies that either x - y ∈ R₊ ∪ {0} or y - x ∈ R₊ ∪ {0}.

Since Q ∩ R₊₊ satisfies the order axioms and Q is a subfield of R, it follows immediately that Q is
an ordered field. However, it is easy to show that the system of complex numbers defined below is
not an ordered field.

We define x > y if x ≥ y and x ≠ y, and define ‘≤’ and ‘<’ to denote the respective inverse
relations of ‘≥’ and ‘>’.

The standard rules of arithmetic that involve inequalities can be derived from the field and order
axioms. The following examples are proved in the Appendix.

• If x > y and w ≥ z, then x + y > y + z

• If x > y > 0 and w ≥ z > 0, then xw > yz.

• Suppose x, y > 0. Then (i) x + y > 0, (ii) (-x) + (-y) < 0, (iii) xy > 0, (iv) x(-y) < 0, (v)
(-x) (-y) > 0.

• For any x ∈ R, define x² ≡ x ٠ x. Then x² > 0 for any x ≠ 0.

• 1 > 0.

• x > 0 implies x^-1 > 0.

• x > y > 0 implies 0 < x^-1 < y^-1. In particular, x > 1 implies x^-1 < 1.

For x, y ∈ R, with x ≥ y, we define max(x, y) = x as the maximum of {x, y} and min(x, y) = y as
the minimum of {x, y} .

We can extend this notation to arbitrary sets of real numbers. If A 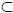R, then max A denotes an
element x ∈ A such that y ∈ A implies y ≤ x. Similarly, min A denotes an element x ∈ A such that
y ∈ A implies y ≥ x.

• For arbitrary sets max A and min A need not exist. Can you provide an example? However,
when they exist, they are always unique.

We define the absolute value of x as |x| = max{x, -x} . The field and order axioms imply the
following properties :

• |x| ≥ 0 and |x| = 0 if and only if x ≠ 0.

• |xy| = |x| |y|

• |x|² = x²

• |x + y| ≤ |x| + |y|

For the remainder of the notes, we freely use all of the standard rules of arithmetic that follow
from the field and order axioms.

(C) Completeness Axiom

To uniquely characterize the real number system, distinguishing it from other ordered fields such
as the rational number system, we require one additional axiom. For any A 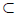R, y ∈ R is an upper
bound for A if x ∈ A implies x ≤ y. And y is a least upper bound for A if y is an upper bound for
A and y ≤ z for any upper bound z of A. We may then state our final axiom as:

Completeness Axiom: Any nonempty set A 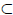R that has an upper bound has a least upper
bound, which we denote by sup A.

Similary, we may define a lower bound and greatest lower bound of A, which we denote by inf A.
Observe that infA = - sup {-x ∈ A} . Therefore the completeness axiom also implies that if A has
a lower bound, it has a greatest lower bound.

• If sup A ∈ A, then max A = supA. Similarly, if inf A ∈ A, then min A = inf A.