Solving Systems of Linear Equations
Solving Systems of Equations
A system of equations is two or more equations taken as a single problem. A
solution to
a system is any point that simultaneously satisfies all equations of the system.
Graphically, a solution to a system is any point of intersection for all the
graphs. If there
are no common points of intersection, then there are no solutions.
Substitution is a useful method for solving systems. Pick one variable and
isolate it, then
substitute for it in the second equation. You should be able to reduce the
second equation
into a single variable, and solve for it. Back-substitute to find the first
variable’ s value .
Not all systems have solutions. Parallel lines never cross, so a system composed
of two
parallel lines has no solution. Or, a parabola and a line could be oriented so
that they do
not cross. Again, so solutions exist. Some systems have multiple solutions. It’s
possible
to orient a parabola and a circle to have 4 intersections, or 4 distinct
solutions.
Graphical methods for locating solutions are sometimes the only means possible
to solve
a system. Systems that combine exponential functions with polynomial functions
( or trig
functions) often cannot be solved by direct algebra.
Systems of Linear Equations in Two Variables
A linear system is a system of linear equations. In this section we will explore
the case in
which we have two equations in two variables, a “2 by 2” for short.
The method of elimination is a nice way to solve these systems. Substitution
works fine,
too. For elimination, rewrite the equations so that the variables are “stacked.”
At this
point, you may:
1. Add the columns if this action cancels out one of the variables, or
2. Multiply one of the equations by a constant (not 0) so that one of the
variables
will cancel upon addition of the columns.
Once you have solved for one variable, plug the result into any of the original
equations
and solve for the other variable. Always graph and double check.
There are three ways to orient two lines in two variables into a single system.
Your text
should illustrate each example. Lines can cross once (an independent system),
not cross
at all (parallel lines, an inconsistent system) or lie atop one another (a
dependent system).
In an inconsistent system, the variables will cancel out simultaneously
(experiment on
your own here), but the constants will remain, leaving you with a statement like
“0 = 2”. Since this
is always false, we conclude so combination of x and y will ever make this
system work. In a dependent case, everything cancels, leaves 0 = 0, which is
always true.
Hence, any point that satisfies one equation will also satisfy the other. You’ll
note that in
the dependent case, one equation is a multiple of the other equation.
Multivariable Linear Systems
A linear system of three equations in three variables is solved in a similar
manner as a “2
by 2.” Elimination works best. These large systems take time and patience.
This will be a short section in which you will work a couple of “3 by 3”
systems. Your
objective is to realize the tedium of algebraically solving large systems, and
the need for
a better method, such as matrices, which we study in a later lesson.
The idea of a “3 by 3” is to select a variable and delete it by taking two pairs
of equations
and eliminating that variable each time. Now you will have a “2 by 2,” which can
be
solved as you learned previously . Once you have solved these two variables, go
back and
solve for the last variable. Your result will be an ordered triple of the form (x,y,z).
Row-
echelon form is the goal, although in practice, you don’t always have to let z
be the last
variable.
Graphically, each equation is a plane in three dimensions. We are trying to
locate where
the three planes intersect, if possible.
Matrices and Systems of Equations
In solving these linear systems, you’ll note that we manipulate the
coefficients, not
necessarily the variables. The variables just hold the place, so to speak. A
matrix is an
array of numbers. We define the size (dimension) of a matrix to be the number of
rows
by the number of columns.
We wish to rewrite our systems into augmented matrix form. This just means we
write
out the coefficients just as we see them (if one is missing, write 0), and also
include a
column for the constants.
The three elementary row operations are given in your text. You already know
these!
You do these “tricks” every time you solve a system by elimination. Our goal is
to use
the row operations to reduce these systems into reduced row echelon format.
Does this form necessarily make solving large systems easier? By hand, probably
not,
especially since one mistake reverberates and throws the whole problem off
track. A
computer algorithm would love this, however. There are other methods for solving
systems by matrices that we will see momentarily. However, in many fields of
mathematics , a knowledge of the basic row operations and of how matrices work
are vital
to understanding the content. For example, matrices are used quite a bit in
Calculus III
and in Differential Equations.
Operations With Matrices
We will now look at matrices as an entity in its own right, and establish its
rules of
arithmetic. Once we have done this, we can move forward for some more advanced
and
clever solution techniques. A calculator is useful. Check your user’s guide to
see how to
enter and manipulate matrices.
First, a definition: Two matrices are equal if and only if each entry is
identical in the
corresponding places.
We can add matrices only if they are the same size. Just add each corresponding
entry.
We can multiply a matrix by a scalar multiple. Just multiply each entry by the
scalar. If
the scalar is negative, we can then define subtraction of two matrices as adding
the
negative of one matrix to another.
Matrix multiplication is a bit more involved. If we wish to multiply AB, where A
and B
are matrices, the number of columns in A must match the number of rows in B. If
this
condition is not met, then the product AB does not exist. Check your text for a
summary
and examples.
If this condition is met, we then form a linear combination of the entries in
the top row of
A and the entries in the first column of B. This means to multiply the first
numbers
together, the second numbers together, and so forth, then add the results. I
think this
concept is best explained by example, so look over them carefully.
Note that if AB exists, BA may or may not exist, and if BA does exist, then AB
may or may
not equal BA. In short, matrix multiplication is not commutative. Therefore,
when we
consider the product AB, we say A “right multiplied” by B, or B “left
multiplied” by A.
The identity matrix is a square matrix with 1s on the main diagonal and 0s
everywhere
else. The identity matrix, abbreviated In, where n is the size of the matrix, acts
like the
number 1 in the context of matrix multiplication. You will note that AI = A and
IA = A.
Inverse Matrices and Systems of Linear Equations
Let A be a square matrix. We wish to multiply A by some other matrix such that
the
product is the identity matrix I. This, then, gives us a way to define division
in the realm
of matrices, as the multiplication by the inverse. We then define the inverse of
a square
matrix A to be ![]() , if and
only if
, if and
only if ![]() and
and
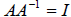 .
.
We will use the calculator for the most part. For the TI-82/83, do the
following:
1. Hit MATRIX, go to EDIT, and enter the entries for your matrix. Just follow
the
prompts. Remember to hit ENTER after each entry.
2. Hit 2nd-QUIT.
3. Hit MATRIX again. By default you’ll be in the NAMES
subheading. Select the
matrix. Hit ENTER.
4. Now type the “x-1” key, and hit ENTER. The result is the inverse of your
original
matrix.
5. A useful trick is to now hit MATH, select NUM, and select FRAC. This will
take
those messy decimals and make fractions out of them.
The idea here is that we can take a system, and decompose it into a matrix
system of the
form AX=B, where A = matrix of coefficients, X = column matrix of variables, and
B =
column matrix of constants. The algebra goes like this :
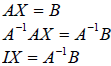 |
given. |
left multiply by
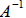 . Note . Note
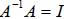 |
|
The answer is 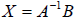 |
Go to your calculator, enter the entries for A and B, then QUIT. Then bring up
A, hit the
x-1key, then bring up B, hit ENTER, and bing, your result! This is a beautiful
method
for really big systems.
| Prev | Next |