Inverse Functions

Section 1.5 Inverse Functions

Objective: In this lesson you learned how to find inverses of functions
graphically and algebraically .

Important Vocabulary Define each term or concept.

Inverse function Let f and g be two functions . If f (g (x)) = x for every x in the domain
of g and g (f (x)) = x for every x in the domain of f, then g is the inverse of the function
f. The function g is denoted by f ^-1.

One-to-one A function f is one-to-one if, for a and b in its domain, f (a) = f (b) implies
a = b.

Horizontal Line Test A function is one-to-one if every horizontal line intersects the
graph of the function at most once.

I. The Inverse of a Function (Pages 120-122) For a function f that is defined by a set of ordered pairs , to form the inverse function of f, . . . interchange the first and second coordinates of each of these ordered pairs. For a function f and its inverse f ^-1, the domain of f is equal to the range of f ^-1 , and the range of f is equal to the domain of f ^-1 . To verify that two functions , f and g, are inverses of each other, . . . find f (g (x)) and g (f (x)). If both of these compositions are equal to x for every x in the domain of the inner function, then the functions are inverses of each other. Example 1: Verify that the functions f (x) = 2x - 3 and 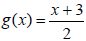are inverses of each other.	What you should learn How to find inverse functions informally and verify that two functions are inverses of each other
II. The Graph of an Inverse Function (Page 123) If the point (a, b) lies on the graph of f , then the point ( b , a ) lies on the graph of f ^-1 and vice versa. The graph of f ^-1is a reflection of the graph of f in the line y = x .	What you should learn How to verify graphically and numerically that two functions are inverses of each other
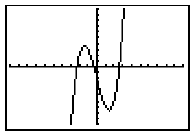
III. The Existence of an Inverse Function (Page 124) A function f has an inverse f ^-1 if and only if . . . f is one-to-one. If a function is one-to-one, that means . . . that no two elements in the domain of the function correspond to the same element in the range of the function. To tell whether a function is one-to-one from its graph, . . . simply use the Horizontal Line Test, that is, check to see that every horizontal line intersects the graph of the function at most once. Example 2: Does the graph of the function at the right have an inverse function? Explain. No, it doesn’t pass the Horizontal Line Test .	What you should learn How to use graphs of functions to decide whether functions have inverses

IV. Finding Inverse Functions Algebraically (Pages 125-126) To find the inverse of a function f algebraically , . . . 1) Use the Horizontal Line Test to decide whether f has an inverse. 2) In the equation for f (x), replace f (x) by y. 3) Interchange the roles of x and y, and solve for y . 4) Replace y by f ^-1(x) in the new equation. 5) Verify that f and f -1 are inverses of each other by showing that f (f ^-1(x)) = x and f ^-1(f(x)) = x. Example 3: Find the inverse (if it exists) of f (x) = 4x - 5 . f ^-1(x) = 0.25x + 1.25	What you should learn How to find inverse functions algebraically
Homework Assignment Page(s) Exercises