College Algebra Chapters 3 & 4 Homework

Show your work or give some kind of justification for each answer!

1. Complete the square to find the vertex of the
parabola
f(x) = 3x² - 5x + 1
f(x) = _______________________(6)
Vertex___________

2. Use synthetic division to show that 3 is a
zero of the function
f(x) = 2x³ - 5x² - 7x +12
(Write a sentence to explain HOW YOU
KNOW that 3 is a zero.) Then use that
information to find exact expressions for all
of the zeros of the function.
________________(7)

3. f(x) = - x⁵ + 2x + 1
g(x) = 7x⁴ + 1
h(x) = - x² - 4
G(x) = x⁷ + x4 + 1
H(x) = 4x³ - x² + 5x
From the list of functions above, identify the
function or functions whose graphs display
the given left-hand and right-hand behavior.

a) Up to the left and down to the right.
__________(3)

b) Down to the left and down to the right.
__________(3)

4. Identify the type of graph (line, circle ,
parabola, etc.) of each of the following:

a) 2x² + 5y² - x - 12 = 0
_______________(2)

b) 7x² + 3x + y - 6 = 0
_______________(2)

5. Find all vertical, horizontal, and slant
asymptotes of these functions.

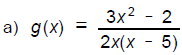
_______________________(6)

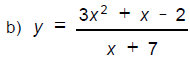
6. Find all of the rational numbers which ,
according to the Rational Zero Test, could
be rational zeros of the function
g(x) = 6x⁵ + x⁴ + 7x³ - 4x² - 5x - 7
______________________________(5)

7. Refer to the function in the previous
problem. According to Descartes' Rule of
Signs , how many positive real zeros and
how many negative real zeros might the
function have?

positive__________(6)
negative__________

8. A candy manufacturer believes that the
demand (D) for a certain kind of candy will
be directly proportional to the amount (in
thousands of dollars) spent on advertising
(A) and inversely proportional to the square
of the price in dollars (p).

a) Write an equation that expresses this
relationship.
_____________(4)

b) If D = 160 units when A = 90 and p = 3,
find the constant of proportionality.
___________(2)

9. Divide (6x³ - 16x² + 17x -10) by (3x - 2)
_________________________________(4)

10. For

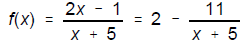
a) As x → -5⁺, f(x) → ____ (3)
b) As x → + ∞, f(x) → ____ (3)

11. Find an equation of the parabola with vertex
at the origin and focus at (-5, 0).
___________________(5)

12. Given: f(x) = 6x⁴ - 5x³ - 15x² - 5x - 21

a) Show that 3 is a upper bound of the real
zeros of the function. (Be sure to include
a sentence explaining your conclusion.)
_______________(3)

b) A graph of the function indicates that
there is a zero between -2 and -1, and
another zero between 2 and 3. Use the
Rational Zero Test to determine the
possible rational zeros that lie between -
2 and -1 or between 2 and 3.
_______________(3)

c) Given that both of the zeros described in
(b) are rational, find these zeros and all
other complex zeros of the function.
_____________________(5)

13. For the hyperbola with the equation

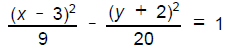
sketch the graph, including the asymptotes,
identifying the vertices, foci, and endpoints
of the transverse and conjugate axes.
( Coordinates may be rounded to the
nearest 0.1)
____________________(6)

14. Find the center, foci, and endpoints of the
axes of the ellipse
3x² + y² + 12x - 2y + 4 = 0
(Coordinates may be rounded to the
nearest 0.1)
____________________(6)

Answers:

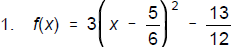
Vertex: (5/6, -13/12)
2. [Syn. div. produces a remainder of 0.]

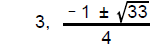
3. a) f b) h
4. a) ellipse b) parabola
5. a) H: y = 3/2 V: x = 0, x= 5
b) S: y= 3x - 20 V: x = -7
6. ±1, ±7, ±½, ±7/2, ±1/3, ±7/3, ±1/6, ±7/6
7. Pos: 1 Neg: 4 or 2 or 0

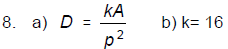
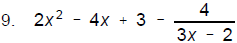
10. a) -∞ b) 2 —
11. y² = -20x

12.
a) [Do syn. div. All numbers in bottom row
are positive .]
b) -3/2 and -7/6; 7/3

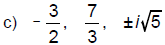
13. Center: (3, -2)
a = 3, b = 4.5, c = 5.4
Vertices: (0, -2), (6, -2)
Ends of conjugate axes: (3, 2.5), (3, -6.5)
Foci: (-2.4, -2), (8.4, -2)

14. Center: (-2, 1)
a = 3, b = 1.7, c = 2.4
Vertices (major axis): (-2, -2), (-2, 4)
Ends of minor axis: (-3.7, 1), (-0.3, 1)
Foci: (-2, -1.4), (-2, 3.4)