RATIONAL NUMBERS

• Rational numbers : are of the form 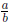  where a and b are both integers and b ≠ 0.



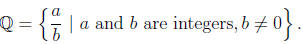
NOTE: Every integer, whole number, and fraction is a rational number.

• Let 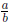  be any rational number and n be a nonzero integer. Then



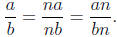
• Let 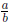be any rational number . Then



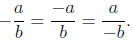
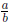• is a positive rational number when either a and b are both positive or when a and b are
both negative .

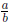•   is a negative rational number when a and b have different signs (one negative and one pos-
itive).

Properties of Rational Number Addition

• Closure Property: Rational number + Rational number = Rational number.
• Commutative Property: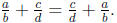
• Associative Property: .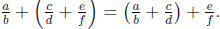
• Identity Property: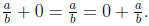

• Additive Inverse Property: For every rational number 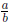, there exists a unique rational
number - 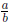such that

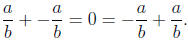
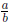- is called the additive inverse .

Properties of Rational Number Multiplication

• Closure Property: Rational number · Rational number = Rational number.
• Commutative Property: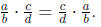
• Associative Property: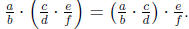
• Identity Property: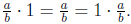
• Multiplicative Inverse Property: For every nonzero rational number , there exists a
unique rational number 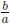  such that



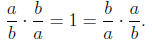
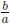  is called the multiplicative inverse or reciprocal .

• Distributive Property :

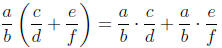
Cross Multiplication of Rational Number Inequality : Let   and 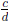  be rational numbers with
b > 0 and d > 0. Then

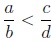if and only if ad < bc:

NOTE: BE CAREFUL!!! Both denominators must be positive in order to use this. DO NOT use
if one of the denominators is negative unless you first the rational number using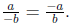

EXAMPLES: Put the appropriate sign (<, =, >) between each pair of rational numbers to make
a true statement.






HOMEWORK: pp 368-369, 2, 4, 5, 7-9, 11, 13, 15, 16