Calculus 102 - Lecture 12
today we will move on to introduce some new integration
techniques.
Very often, we will need to integrate a very special type of
function which is called rational functions . Here is the definition.
Definition 1 A rational function is the function of the form
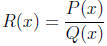
. where P(x) and Q(x) are both polynomials.
The way we will apply is called method of partial fraction.
Definition 2 (Method of Partial Fraction) The method of partial
fraction is the algebraic technique that decomposes R(x) into a
sum of terms :
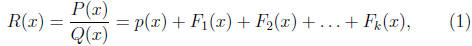
where p(x) is a polynomial and Fi(x) is a fraction that
can be integrated
without difficulties.
We know from basic algebra that the only inreducible polynomials
with coefficient in R are quadratic and linear polynomials. Believe
it or now, Using this principle, we can show every rational function
can be written as equation (1), with Fi(x) being either

. or

. Fractions of these forms are called partial fractions.
Equation(1)
is called partial fraction decomposition.
We need to learn to deal with the first type of partial fractions
now. We need a Definition first.
Definition 3 A fraction 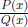 is called proper if
and only if the degree
is called proper if
and only if the degree
of P(x) is strictly less than that of Q(x).
The harder part is to deal with proper fractions, but now we need
to deal with fraction that is not proper. The technique is called long
division.
Please see the following examples.
Example 1 please find 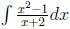
Example 2 please find 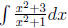
So I need you to remember now, the very first step to integrate a
rational function is to apply long division to reduce the improper
fraction to proper fraction.
.
Then we need to factorize the denominator. As we just said, the only
inreducible polynomial is quadratic and linear polynomial, so you
should express the bottom as the product of linear and quadratic
IRREDUCIBLE polynomials.
The first rule you should apply is
Rule 1 The part of the partial fraction decompsition that corresponds
to the linear factor ax + b with multiplicity n is
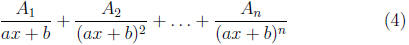
of course the capital Ai is constants.
Example 3 please find 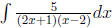
Example 4 please find 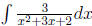 .
.
Here you will have to FACTORIZE the denominator yourself .
Let us see another more difficult problem.
Example 5 please find 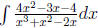
The idea is
• you can list the factors according to rule 1,
• and then you need to find the common denominator of these
partial fractions which is of course the original denominator(
believe or not),
• then write the partial fractions using this common denominator,
• arrange the terms and match the coefficients with that of the
original numerator, you will get a list of simultaneous equations .
• solve them to get the coefficient Ai.
• integrate it.
Example 6 please find
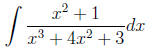
Example 7 please find
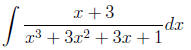
Example 8 please find
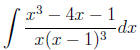
Example 9 please find
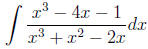
Rule 2 The part of the partial fraction decompsition that
corresponds
to the quadratic factor ax2 + bx + c with multiplicity n is
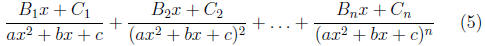
of course the capital Bi and Ci is constants.
Here sometimes you will see very complicated examples if you were
given some very large multiplicities for the quadratic factor. I was
tortured that way when I first learnt this. But you can be assured
it will not happen to you.
What you need to pay attention here is that the numerator is a linear
polynomial instead of a constant.
Do not confuse yourself with the linear factor case.
Here is several examples for you to do.
Example 10
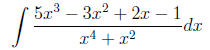
Example 11
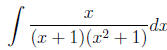
Example 12
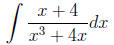
As the book suggests, you might consider using the
following formula ,
the reason I put them here is to help you do problem faster.
But I will assume you can find it yourself when you see them in the
problem.
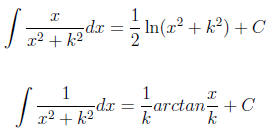
| Prev | Next |