Factoring the Sum and Difference of Cubes
Forumulas
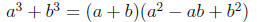
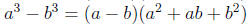
Expand these formulas to show that they are correct.
Example 1 Factor: y^3 - 8
Example 2 Factor: z^3 + 125
Recalling the Difference of Squares Formula
Difference of Squares:
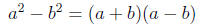
Example 3 Factor: 25x^2 - 81
General Rules for Factoring
1. Factor out the GCF .
2. Identify whether the polynomial has two terms , three terms, or more
than three terms.
3. If the polynomial has more than three terms, try factoring by grouping .
4. If the polynomial has three terms, check first for a perfect square
trinomial.
Otherwise, factor the trinomial with the grouping method (or the trial and error
method).
5. If the polynomial has two terms, determine if it fits the pattern for
(a) a Difference of squares, or
(b) a Difference of cubes, or
(c) A sum of cubes .
6. Be sure to factor completely.
7. Check your answer by multiplying .
Example 4 Factor: 3ac + ad - 3bc - bd
Example 5 Factor: -2x^2 + 8x - 8
Example 6 Factor: -p^3 - 5p^2 - 4p
Steps for Factoring Trinomials by Grouping
Your trinomial has the form ax^2 + bx + c.
1. Identify a, b, and c.
2. Find m and n such that mn = ac and m + n = b.
3. Rewrite your original trinomial as ax^2 + mx + nx + c.
4. Group the first two terms and the last two terms and factor each of them.
5. Finish by factoring the common binomial from the two resulting terms.
Example 7 Factor: 7p^2 - 29p + 4
1. Identify a, b, and c.
2. Find m and n such that mn = ac and m + n = b.
3. Rewrite your original trinomial as ax^2 + mx + nx + c.
4. Group the first two terms and the last two terms and
factor each of
them.
5. Finish by factoring the common binomial from the two resulting terms.
| Prev | Next |