Abstract Algebra II Course Goals
Catalog description: This course continues the
study of abstract algebra and is focused mainly on
groups, with some exploration of rings and fields as time allows. Group
theoretic topics include subgroups, normal
subgroups and quotient groups , and some counting principles. A wide variety of
examples will be explored.
Learning Objectives:
I. Algebra fundamentals
Students will be able to:
• Define equivalence relation and equivalence class and determine, with complete
justification, whether or
not a given relation is an equivalence relation and, if so, identify equivalence
classes.
• State the Well- Ordering Principle of the positive integers and use it in a
proof.
• State and use the First and Second Form of Mathematical Induction and it in a
proof.
• Define function, one-to-one function, and onto-function; and identify examples
and non-examples of each.
• Define left-inverse, right-inverse and inverse of a function; and identify
examples and non-examples of
each, and prove the equivalence of one-to-one and existence of a left-inverse,
and the equivalence of onto
with existence of a right inverse.
II. Groups
Students will be able to:
• Demonstrate familiarity with the definition of a group and be able to test a
set with binary operation to
determine if it is a group.
• Construct a Cayley table for a group.
• Demonstrate familiarity with the common groups (Zn, R*, U(n),
GL(2,R), Dn etc)
• Compute the order of a group , the order of a subgroup, and the order of an
element.
• Identify subgroups of a given group.
• Identify cyclic groups and apply the fundamental theorem of cyclic groups.
• Demonstrate familiarity with permutation groups and be able to decompose
permutations into 2-cycles.
• Define the concepts of homomorphism, isomorphism, and automorphism and check
whether a given
function defines one of these.
• Prove the common properties of homomorphisms (e.g. that if K is a subgroup of
G then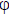 
(K) is a subgroup
of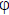 
(G) ).
• Prove that Aut(G) is a group and compute Aut(G) for given a given G.
• Define the external direct product and be able to compute the direct product
of groups.
• Apply Lagrange’s theorem.
• Define normal subgroups and be able to prove that given subgroups are normal.
• State and apply the fundamental theorem of finite Abelian groups.
III. Rings
Students will be able to:
• Give a definition of ring and cite a variety of common examples and
non-examples (finite and infinite,
polynomials , and matrices)
IV. Fields
Students will be able to:
• Give the definition of field and cite a variety of
common examples and non-examples (characteristic 0 and
characteristic p, polynomials , matrices)
IV. Applications
Students will be able to:
• Demonstrate familiarity with some of the applications of algebra to other
fields, e.g. cryptography.
Approved: 05-08
| Prev | Next |