Math 41 Study Guide
4.1 Polynomial Functions and their Graphs
• End behavior:
o
Look at leading coefficient /exponent and check sign
o
If polynomial is factored, check sign of each factor and multiply
• Graphing a polynomial:
o
Factor
o
Find x- and y-intercepts
o
Find end behavior
o
Either use test points between the intercepts or memorize the shape around zeros
depending on the multiplicity:
— If multiplicity is 1, then it crosses the x-axis in a straight line
— If multiplicity is even, then it turns back around
— If multiplicity is odd > 1, then it ”squiggles” through the x-axis
4.2 Dividing Polynomials
• Long Division: Make sure to fill in missing powers
• Synthetic Division: Only works for division by (x − c). Again make sure to
fill in 0’s
for missing powers
• Remainder Theorem: to find P(c) carry out a synthetic division for c, the
remainder
is P(c)
• Factor Theorem : c is a zero of P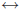 
(x − c) is a factor of P(x)
4.3 Real Zeros of Polynomials
• Rational Zeros Theorem: The possible rational zeros of a polynomial are of the
form
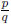where p is a factor of the constant coefficient
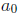and q is a factor of the
leading
coefficient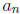 
• How to find all zeros of a polynomial:
o
Try previous factoring methods like substitution or grouping , if this does not
work
then:
o
List all possible rational zeros using the Rational Zeros Theorem
o
Test the possible zeros
o
If you find a zero, factor it out
o
Repeat from the top until your polynomial is quadratic, then factor/complete the
square/ quadratic formula
4.4 Complex Zeros and the Fundamental Theorem of Algebra
• Fundamental Theorem of Algebra: every polynomial of degree n has precisely n
zeros
(zeros of multiplicity k are counted k times )
• Conjugate Zeros Theorem: If a complex number is a zero of polynomial with real
coefficient, then its conjugate is also a zero
4.5 Rational Functions
• Horizontal asymptotes: n is the degree of the numerator, m is the degree of
the denominator
o
n > m: no horizontal asymptote
o
n = m: horizontal asymptote is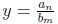 
o
n < m: horizontal asymptote is y = 0
• Vertical asymptotes: zeros of the denominator (that do not cancel with the
numerator)
• Graphing rational functions:
o
Factor numerator and denominator
o
Find x- and y-intercepts
o
Find horizontal and vertical asymptotes
o
Either use test points between intercepts/vertical asymptotes or use the shape
around vertical asymptotes/intercepts to determine the shape of the graph
• Slant asymptote: only exists if the degree of the numerator is one greater
than the
degree of the denominator: use long/synthetic division
5.1 Exponential Functions
• f(x) = ax, memorize the graph:
o
Horizontal asymptote y = 0
o
no vertical asymptote
o
Domain = (−∞,∞)
o
Range = (0,∞)
• Compound interest formula: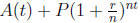 
• Continuously compounded interest: A(t) = ert
5.2 Logarithmic Functions
• Definition of logarithm: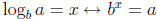 
• Properties:
• 
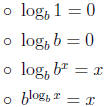
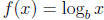, memorize the graph:
o
Vertical asymptote: x = 0
o
no horizontal asymptote
o
Domain = (0,∞)
o
Range = (−∞,∞)
• Finding the domain of logarithmic function: logarithms only defined for
positive numbers
• Common log :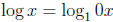 
• Natural log: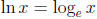 
5.3 Laws of Logarithms
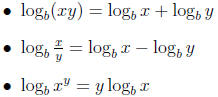
• no laws for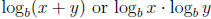 
• Change of base: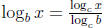 
where c can be any
positive number
5.4 Exponential and Logarithmic Equations
• Solving exponential equations:
o Isolate the exponential term on one side
o Take logarithm of both sides:
— If there is only one exponential term, use that base for the log
— If there is an exponential term on both sides, use either the common or
natural
log
o Pull the exponent to the front and solve the equation
• Solving logarithmic equations:
o If there are multiple logarithmic terms, combine them into one using
logarithmic
laws
o Isolate the logarithmic term on one side
o Raise the base of the logarithm to the left and the right side of the equation
o Use the property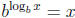 
to get rid of the log
o Solve the equation
• Two special cases of exponential equations:
o Combination of exponential and polynomial terms: try to factor
o Sum of multiple exponential terms: try to use substitution
5.5 Modeling with Exponential and Logarithmic Functions
• Exponential growth model: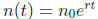 
• To solve any problem you usually have to find
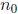and r
• Formulas and logarithmic scales
6.1 Angle Measure
• Relationship between Degrees and Radians:
o convert from degrees to radians by multiplying by
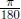
o convert from radians to degrees by multiplying by
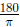
• Coterminal angles: Angle between 0° and 360° degrees (or 0 and 2π )
• Length of a circular arc: s = rθ ( θ in rad)
• Area of a circular sector: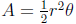 
( θ in rad)
• Linear Speed and Angular Spee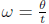d: 
and
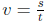
• Relationship between linear and angular speed: v = rω
6.2 Trigonometry of Right Triangles
• Trigonometric Ratios:
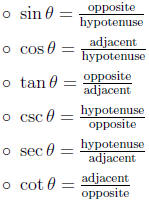
• Values of the trig ratios for angles 30° , 45° and 60°
• Solving right triangles
| Prev | Next |