Adding and Subtracting Polynomials
I. Types of Polynomials
A. Basic Definitions
1. In the term bx m, b is called the coefficient, x is
called the variable, and m is
called the exponent on the variable .
2. Whenever we have just one term, that term is called a monomial.
3. Examples
a. 6x The coefficient is 6, the variable is x , the
exponent on the variable
is 1.
b. –17 The coefficient is –17, the variable is x (or anything else you
would like ), and the exponent on the variable is 0.
B. A polynomial is a sum of monomials.
Examples
1. 15x3 – 8x2 + 5x – 7
2. 28y12 + 16y6 – 25y3 + 4
C. The degree of a term is the sum of the exponents on the variables of the term.
D. The degree of a polynomial is the highest degree of any of the terms of the
polynomial.
E. A polynomial is written in standard form when the term with the highest
degree is
written first and the degrees of the terms go in descending order .
F. When a polynomial is written in standard form, the first coefficient is
called the
leading coefficient. Then if the last term has no variable, it is called a
constant term.
II. Names of Polynomials
A. A polynomial of one term is called a monomial.
B. A polynomial of two terms is called a binomial .
C. A polynomial of three terms is called a trinomial .
D. A polynomial of more than three terms is just called a polynomial.
A. We simplify polynomials by using the distributive, associative, and
commutative
properties to combine the like terms .
B. Examples – simplify each polynomial.
1. 3y – 2y – y
Answer: 0
2. 3x3 – x2 + x3 – 2x2
3x3 + x3 – x2 – 2x2
Answer: 4x3 – 3x2
3. Now you try one: -2y – 1 – 3y – 4
Answer: −5y – 5
4.
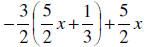
First we distribute to get :
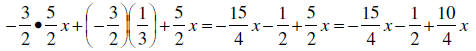
Answer :
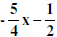
5. Now you try one: −3.2(2.1 – 1.2w) + 2.1w
Answer: 5.94w – 6.72
6. (8t5 + 3t3 + 5t) − (19t5 − 6t3 + t)
On the first parentheses , we distribute +1, which effectively does what?
On the second parentheses, we distribute −1, which effectively does what?
So we get:
8t5 + 3t3 + 5t − 19t5 + 6t3 − t
OR
Answer: −11t5 + 9t3 + 4t
7. Now you try one: (8m2 − 7m) − (3m2 + 7m − 6)
Answer: 5m2 −14m + 6
8. Note that this: Subtract
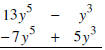
Means the same thing as this: (13y5 − y3) − (−7y5 + 5y3)
9. As you complete more years of education, you can count on a greater
income. The bar graph (bottom of the right-hand column, page 330) shows
the median, or middle-most, annual income for Americans, by level of
education, in 2004.
Here are polynomial models that describe the median annual income for men,
M, and for women, W, who have completed x years of education:
M = 177x2 + 288x + 7075
W = 255x2 – 2956x + 24,336
M = −18x3 + 923x2 – 9603 x + 48,446
W = 17x3 – 450x2 + 6392x – 14,764
Use the equations defined by polynomials of degree 3 to find a mathematical
model for M – W (page 331, #104a)
A polynomial of degree 3 means that the highest exponent on the polynomial
is 3. This is the case with the second set of formulas . So we have:
M – W = (−18x3 + 923x2 – 9603 x + 48,446) – (17x3 – 450x2 + 6392x – 14,764)
M – W = −18x3 + 923x2 – 9603 x + 48,446 – 17x3 + 450x2 – 6392x + 14,764
Answer: M – W = −35x3 + 1373x2 – 15,995x + 63,210
b. According to the model in part (a), what is the difference in median annual
income between men and women with 16 years of education?
Remember that x represents the number of years of education. So we need
to substitute 16 in for x in the answer that we got in part (a).
M – W = −35(16)3 + 1373(16)2 – 15,995(16) + 63,210
M – W = −35(4096) + 1373(256) – 15,995(16) + 63,210
M – W = −143,360 + 351,488 – 255,920 + 63,210
M – W = 15,418
Answer: The difference in median annual income between men and women
with 16 years of education is $15,418.
c. According to the data displayed by the graph on page 330, what is the actual
difference in the median annual income between men and women with 16
years of education? Did the model in part (b) underestimate or overestimate
this difference? By how much?
Looking at the bar graph on page 330, we see that the median annual income
for men with 16 years of education is $57,220; for women it is $41,681. The
difference is
57,220 – 41,681 = 15,539
So our number in part (b) is an underestimate of $121 (15,539 – 15,418).
| Prev | Next |