Investigating Factors and Multiples
I. Materials Needed
II. Factors and Multiples
A. Forming Rectangles to Find Factors
1. Using 6 cubes , make two different rectangles . (NOTE: for this activity,
since a
2 x 5 rectangle made with 10 squares is congruent to a 5 x 2 rectangle, the
two rectangles will not be considered "different".)
What are the dimensions of one of the rectangle?
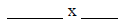
Sketch your model.
What are the dimensions of the other rectangle?
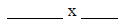
Sketch your model.
2. The dimensions of the rectangles made with six squares are the factors of 6.
List the factors of 6 is ascending order 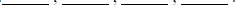
3. Find all the factors of 16 by making rectangles. Sketch your models.
4. Find all the factors of 18 by making rectangles. Sketch your models.
B. When we write 2 x 3 = 6, we can say: "Two and three are
factors of six." So, 6 is a
multiple of 2 and a multiple of 3. When we write 6 ÷ 2 = 3, we can say that 6 is
divisible by 2 or when we write 6 ÷ 3 = 2, we can say that 6 is divisible by 3.
Therefore,
2 and 3 are divisors of six.
Write statements using the words factor, multiple, divisor, and divisible
related to
"4 x 6 = 24".
III. Even and Odd
A. The natural numbers can be represented geometrically with patterns of squares
involving
one or two rows. The first five numbers are illustrated below. Continue the
pattern
through 13. Make a sketch of your models.
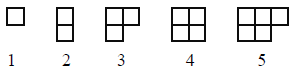
B. Describe how the models for 1, 3, 5, 7, and so on differ from the models for
2, 4, 6, 8, and
so on. The characteristic you described for 2, 4, 6, and 8 are called even
numbers. The
others are called odd numbers. Using your characteristic, describe why 10 is an
even
number.
C. Modeling Even Numbers: The first three even numbers are
modeled below.
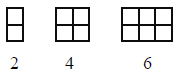
1. Draw the figure for the sixth even number.
2. What is the sixth even number?
3. Describe, in words, how the 120th even number would look.
4. What is the 120th even number?
5. Describe, in words, how the nth even number would look.
6. What mathematical expression represents the nth even number?
D. Modeling Odd Numbers: The first three odd numbers are modeled below.
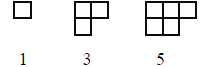
1. Draw the figures for the sixth and seventh odd numbers.
2. What is the sixth odd number? the seventh odd number?
3. Describe, in words, how the 17th odd number would look?
4. What is the 17th odd number?
5. Describe how the 40th, 100th, and nth odd numbers would
look.
6. What is the 40th odd number? the 100th odd number?
the 100th odd number?
7. What mathematical expression represents the nth odd number?
E. Determine whether each of the following is even or odd. Explain your
reasoning and
justify by drawing pictures to illustrate your explanation.
1. The sum of two even numbers
2. The sum of two odd numbers
3. The sum of an even number and an odd number
4 The sum of three odd numbers
5. The sum of any three consecutive natural numbers
F. Finding GCD’s and LCM’s
Find the following by the method of intersection of sets of divisors.
1. GCD(24, 27)
2. GCD(14, 22)
3. GCD((48, 72)
Find the following by the method of intersection of sets of multiples.
4. LCM(24, 27)
5. LCM(14, 22)
6. LCM(48, 72)
Use the above results for the following.
7. Find the product of the GCD and LCM of 24 and 27.
8. What is the product of 24 x 27?
9. What is the relationship between the answers to #8 and #9?
10. Show that the same relationship exists for the numbers 14 & 22 and for 48 &
72.
11. If the GCD of 2268 and 77,175 is 63, find the LCM of 2268 and 77,175.
Find the GCD of the following pairs of numbers by the
method of prime factorization.
12. 1500 and 450
13. 2695 and 3500
14. 12,600 and 41,580
Find the LCM of the following pairs of numbers by the method of prime
factorization.
15. 1500 and 450
16. 2695 and 3500
17. 12,600 and 41,580
A local bakery celebrated its one-year anniversary on Saturday. On that day,
every 4th customer received a free
cookie. Every 6th customer received a free muffin. Every 10th customer received
a free mini-cake.
18. Casey was the first customer to receive both a free cookie and a free
muffin. What number
customer was Casey? (Show how you got your answer.)
19. Tom entered the bakery and only got a free cookie. What number customer
could Tom have
been? (Show how you got your answer.)
20. Sarah was the first customer to receive two free goodies. What did she
receive and what number
customer was she? (Show how you got your answer.)
21. What free goodies did the 30th customer receive? (Show how you got your
answer.)
22. On that day, the bakery gave away a total of 29 free cookies. What was the
total number of free
muffins given away that day? (Show how you got your answer.)
30. Did anyone receive 3 free goodies? If so, what number customer was it? If
not, what number
customer would it have been? (Show how you got your answer.)
| Prev | Next |