APPLICATIONS OF THE ORDER FUNCTION

In this lecture we will explore several applications of order functions including formulas
for GCDs and LCMs , a method of showing certain numbers are irrational, and counting the
number of zeros at the end of n!.

1. Review

We begin with a review of results from the previous lecture .

Definition 1. If m is a nonzero integer and if p is a prime, then Ord_p(m) is the largest
integer k such that p^k divides m.

Proposition 2. Let p be a prime and m be a nonzero integer. Then p | m if and only if
Ord_p(m) > 0.

Proposition 3. Let m be a nonzero integer, and p be a prime. Then Ord_p(m) = k if and
only if m = up^k for some u relatively prime to m.

Proposition 4. If p is a prime and u is an integer such that p 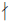u, then Ord_p(up^k) = k.

Proposition 5. Let p be a prime. If a, b ∈ Z are non-zero then

Ord_p(ab) = Ord_p(a) + Ord_p(b):

More generally, if each 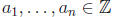is nonzero then

Ord_p(a₁… a_n) = Ord_p(a₁) +… + Ord_p(a_n):

Proposition 6. If a ∈ Z is non-zero and if k ≥ 0 then

Ord_p(a^k ) = k Ord_p(a):

Proposition 7. Suppose 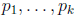are distinct primes. Then

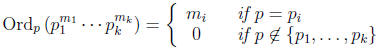
Proposition 8 (Product formula). Let n be a positive integer, and let 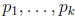be a nite
sequence of distinct primes that includes every prime divisor of n . Then

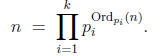
Exercise 1. Let n be a positive integer . Show that n is a perfect square if and only if
2 | Ord_p(n) for all primes p. Hint: one direction uses the product formula.

2. Additional Results

Here are a few useful formulas involving order.

Proposition 9. If n ∈ Z is nonzero, and p is a prime, then

Ord_p(-n) = Ord_p(n):

Proposition 10. Suppose m and n are positive integers. If Ord_p(m) = Ord_p(n) for all
primes p, then m = n.

Proof. Let 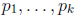be a finite sequence of distinct primes that include all primes dividing
m and n. By the product formula

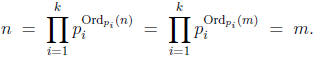
The connection between the order functions and divisibility is described by the following
theorem.

Theorem 11. Suppose m, n ∈ Z are both non-zero. Then

m | n   if and only if   Ord_p(m) ≤ Ord_p(n) for all primes p.

Remark. Since Ord_p(m) = Ord_p(n) = 0 for all p not dividing m and n, we only need to check
the right-hand condition for p dividing m or dividing n.

Proof. Suppose m | n. Then n = ml for some l ∈ Z. So Ord_p(n) = Ord_p(m) + Ord_p(l) for
all primes p. This implies that Ord_p(m) ≤ Ord_p(n) for all primes p.

Now suppose that Ord_p(m) ≤ Ord_p(n) for all primes p. First assume that m and n are
positive. Let 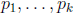be a nite sequence of distinct primes that includes all prime divisors
of m and n. Let 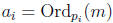and 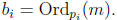By assumption, 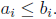Define l ∈ Z by
the formula

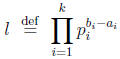
By Proposition 7, 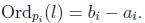Thus, for all p_i in the sequence

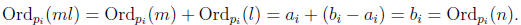
For p not in the sequence,

Ord_p(ml) = Ord_p(m) + Ord_p(l) = 0 + 0 = 0 = Ord_p(n):

By Proposition 10, ml = n. So m | n as desired.

If m and n are not both positive, then Ord_p(|m|) Ord_p(|n|) for all primes p (Proposi-
tion 9). Thus |m| | |n| by the above argument. But |m| | |n| implies that m | n.

Corollary 12. Suppose a, b, d ∈ Z are non-zero. Then d is a common divisor of a and b if
and only if Ord_p(d) ≤ min (Ord_p(a), Ord_p(b)) for all primes p.

Corollary 13. Suppose a and b are non-zero integers. Let 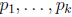be a finite sequence of
distinct primes that include all divisors of a and b. Then

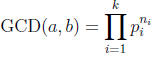
where
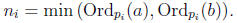
Proof. Let 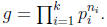Proposition 7 and definition of n_i,

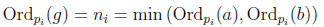
for all p_i in the finite sequence, and Ord_p(g) = 0 for other p. Thus

Ord_p(g) = min (Ord_p(a), Ord_p(b))

for all primes p. By Corollary 12, g is a common divisor .

Suppose d is any other positive divisor. By Corollary 12,

Ord_p(d) ≤ min (Ord_p(a), Ord_p(b)) = Ord_p(g)

for all primes p. Thus d | g by Theorem 11. Thus d ≤ g. This shows that g is the greatest
common divisor .

3. Least common multiplies (LCM)

We start with a criterion for a number to be a common multiple.

Proposition 14. Suppose a, b,m ∈ Z are non-zero. Then m is a common multiple of a
and b if and only if Ord_p(m) ≥ max (Ord_p(a), Ord_p(b)) for all primes p.

Proof. If m is a common multiple of a and b , then a | m and b | m. By Theorem 11, this
means that Ord_p(a) ≤ Ord_p(m) and Ord_p(b) ≤ Ord_p(m) for all primes p. In other words,
Ord_p(m) ≥ max (Ord_p(a), Ord_p(b)) for all primes p.

If Ord_p(m) ≥ max (Ord_p(a), Ord_p(b)) for all primes p, then Ord_p(a) ≤ Ord_p(m) and
Ord_p(a) ≤ Ord_p(m). By Theorem 11, m is a common multiple of a and b.

Theorem 15. Suppose a and b are non-zero integers. Then there is a unique least common
positive multiple (LCM) M of a and b. Furthermore, an integer c is a common multiples of
a and b if and only if c is a multiple of M. The least common (positive) multiple M is given
by the formula

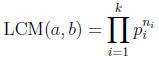
where 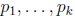is a finite sequence of distinct primes that include all divisors of a and b.
and

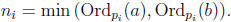
Proof. Let 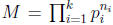where n_i and p_i are as above. We will show that M has all the
desired properties. Obviously M is positive (closure under multiplication). By Proposition 7
and definition of n_i,

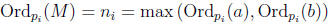
for all p_i in the finite sequence, and Ord_p(g) = 0 for other p. Thus

Ord_p(M) = max (Ord_p(a), Ord_p(b))

for all primes p. By the previous proposition , M is a common multiple.
Suppose c is any other common multiple. By Corollary 12,

Ord_p(c) ≥ max (Ord_p(a), Ord_p(b)) = Ord_p(M)

for all primes p. Thus M | c by Theorem 11. A similar argument shows that if M | c then
c is a common multiple. So c is a common multiple of a and b if and only if c is a multiple
of M.

In particular, if c is a positive common multiple, then M | c, so M ≤ c. Thus M is smaller
than any other common multiple. So M is a least common multiple. Uniqueness is obvious
(M ≤ M' and M' ≤ M implies M = M').

Here is an interesting formula relating LCM (a, b) and GCD(a, b) :

Theorem 16. Let a and b be positive integers. Then

LCM(a, b) GCD(a, b) = ab

Proof. For any prime p, let m_p = Ord_p(a) and n_p = Ord_p(b). Then, by Corollary 13,
Theorem 15, and Proposition 7,

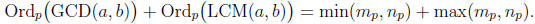
By the following lemma,

min(m_p, n_p) + max(m_p, n_p) = m_p + n_p = Ord_p(a) + Ord_p(b)

Thus LCM(a, b) GCD(a, b) and ab have the same order (for all p). By Proposition 10, they
are equal.

Lemma 17. Let m, n ∈ Z. Then min(m, n) + max(m, n) = m + n.

Exercise 2. Prove the above lemma.

Remark. This lemma does not use any special properties of Z . In fact, it is true of m, n ∈ U
where U is any linearly ordered set, and + is any commutative binary operation on U.

This above theorem generalizes:

Proposition 18. Let a and b be non-zero integers. Then

LCM(a, b) GCD(a, b) = |ab|.

Proof. Apply Theorem 16 to |a| and |b|. Then use the following lemma.

Lemma 19. Let a and b be non-zero integers. Then

LCM(a, b) = LCM (|a|, |b|),  GCD(a, b) = GCD (|a|, |b|).

Exercise 3. Prove the above by showing that a and b have the same common divisors (and
multiples) as |a| and |b|.