Math 308 Practice Final Exam
Problem 1: Solving a linear equation
Given matrix
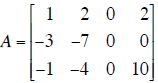
and vector
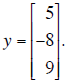
(a) Solve Ax = y (if the equation is consistent ) and write
the general solution x in
(vector) parametric form.
Write a basis for the null space of A. Basis = ___________________
(b) What is the dimension of the range of A? Dimension = _____
(c) Is y in the span of the row vectors of A? Yes? ___ No? ___
Problem 2: Conclusions from echelon form.
In each case, we start with a matrix A and vector and tell
what one will get by reducing
the augmented matrix of the system Ax = y to echelon form. Answer the questions
in
each case using this information. It is possible some equations will have no
solution.
| A | y | Echelon form of augmented matrix of Ax = y. |
|
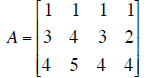 |
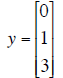 |
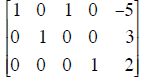 |
|
| (a) Write the general solution for Ax
= y in (vector) parametric form Solution: (b) What is the dimension of the null space of A? Dimension = ____ (c) Write down a basis for the null space of A.
Basis = |
|||
| B | z | Echelon form of augmented matrix of Bx = z. | |
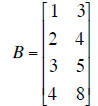 |
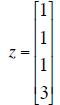 |
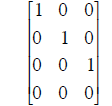 |
|
| (a) Write the general solution for Bx
= z in (vector) parametric form Solution: (b) What is the dimension of the null space of B? Dimension = ______ (c) Write down a basis for the null space of B. Basis = (d) Is z in the range of B? Yes? No? (e) What is the dimension of the range of B? Dimension = ______ (f) Write down a basis of the range of B. Basis = (g) Are the columns of B independent? Yes? No? |
|||
| C | Reduced row echelon form of C. | ||
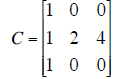 |
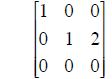 |
||
| (a) Is C invertible?
Yes? ___ No? ___ (b) Are the columns of C independent? Yes? ___ No? ___ (c) Write down a basis for the null space of C. |
|||
Problem 3: Compute matrix products and inverses
Compute the stated matrix products (if defined) for these matrices.
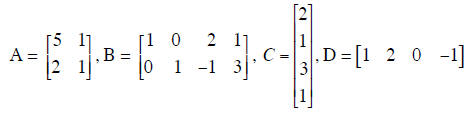
Compute each of the following matrix products or other matrices (if defined):
| A-1 | C-1 |
| AB | BA |
| CD | BC |
| CDT | CTD |
Problem 4: Find the eigenvalues and eigenvectors
Find the eigenvalues and eigenvectors of matrix
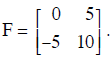
If possible, diagonalize F, i.e., write F = UDV, where D is diagonal.
U =_____________ D = ________ V =_______________
Problem 5: Given the eigenvalues find the eigenvectors
Given that 1 and -3 are the eigenvalues of the matrix
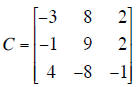 find
the
find
the
eigenvectors of this matrix. Hint: First find whether
there is a third eigenvalue. If you
compute the determinant of C, knowing 2 eigenvalues, you can find the third root
of the
characteristic polynomial without computing det(C - λI).
If possible, diagonalize C, i.e., write C = MDN,
where D is diagonal. You DO NOT
need to compute the inverse of any matrix in this problem. If a matrix is the
inverse of a
known matrix, just write it as the inverse.
M =________ D =______________ N =__________________
Problem 6: Compute orthogonal projections
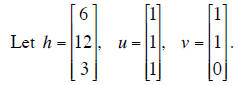
(a) Compute m = the projection of h on Span({u}). (The
formula should be computed
numerically , but you need not simplify fractions , etc., in your answer.)
(b) Compute g = the projection of h on Span({u, v}).
(The formula should be
computed
numerically , but you need not simplify fractions , etc., in your answer.)
Problem 7: Matrix of Linear Transformation
(a) If T is the linear transformation of R2 that rotates the plane by an angle
so that the
point (1, 0) is rotated to (3/5, 4/5). What is the matrix A of this
transformation?
(b) Is the matrix A an orthogonal matrix? Yes? ___ No? ___
(c) Is the matrix 2A an orthogonal matrix? Yes? ___
No? ___
Show why in both cases.
(d) Given the vector
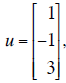 if
x is a vector in R3, then let T(x) = (u ∙ x)u. Is T a linear
if
x is a vector in R3, then let T(x) = (u ∙ x)u. Is T a linear
transformation? If so, what is its matrix (with respect to
the standard basis).
Problem 8: Least squares solution
You have the following data for variables x , y, z
| x | y | z |
| 0 | 0 | 3 |
| 1 | 0 | 4 |
| 0 | 1 | 4 |
| 1 | 1 | 1 |
(a) Now suppose that you want to fit this data to a
function z = a + bx + cy, where, a, b, c
are some constants that you need to solve for. Write a system of equations for
variables a, b, c that can be solved if there is an exact fit of the function to
the data.
(b) Find the lease-squares "solution" a, b, c to this system and check the
values of z = a +
bx + cy at the data points to see how close a fit it is.
Least squares solution : z = ___ + ___ x + ___ y
| Prev | Next |