Linear Algebra and Differential Equations
Linear Algebra and Differential Equations
Linear Algebra and Differential Equations are the fundamental mathematical tools
for sophisticated
mathematical modeling and applications in the natural and social sciences. By
now you have had significant
experience using algebra to formulate and solve problems -- particularly when
there is only a single
variable to work with. You have also had some experience setting up and solving
systems of equations
which involve more than one unknown. Through our study of linear algebra we will
learn techniques for
computing with matrices and vectors. This turns out to be pretty handy in the
study of differential equations
(and also in studying Multivariable Calculus). Differential equations are simply
equations which involve
derivatives. You have been working with these in Calculus while developing your
concept of derivatives
and techniques of integration. In this course, we will classify and learn to
solve ordinary differential
equations: equations which involve derivatives of functions of just one
dependent variable. We will see
some applications in the sciences, but we will focus on the mathematical theory,
concepts, and tools that
are required to analyze and solve simple applications.
According to the course description in the university catalogue, our study will
address the following topics
(although not necessarily in the order listed): linear systems, abstract vector
spaces, matrices through eigenvalues
and eigenvectors, solutions of ordinary differential equations, Laplace
transforms, and first order
systems.
Prerequisite
Successful completion of Differential and Integral Calculus is required for this
course. This means that
you have taken and passed MATH 1220 or earned a score of 5 on a BC Calculus
exam.
Materials
We will use the textbook called “Differential Equations: A Systems Approach” by
Goldberg and Potter.
This means that group projects and homework exercises will be assigned from this
book, and that I will
allow the authors’ approach to the subject guide ours. You may be interested in
using a book called “Introduction
to Linear Algebra and Differential Equations” by Dettman (published by Dover)
because it covers
what we will be studying in class and it only costs about $15. This book is not
required! We will also
be making use of MATLAB. You need to have a computer account and access to the
labs which have
MATLAB installed (ENGR 305, Ag Sci 119). You may purchase a student version of
MATLAB at the bookstore
for your own computer, but this is not required -- the cost is about $100. You
are free to use whatever
calculator you wish to use, but no calculators are allowed on in-class quizzes.
Assignments
We will assign and review homework exercises each class day, but I will not
collect or grade these. A quiz
on homework problems will be given at the beginning of class each Friday. There
will be 11 quizzes offered
in total, but your lowest score will be dropped to compute your final grade. We
will have 3 group
assignments due the 3rd, 8th, and 15th week of the term. I will hand out details
on these as they are assigned;
however, you can expect to hand in a written component (one paper per group) and
do a short
presentation of your work in class. Also, there will be
one midterm exam and one final exam. Our midterm
will be on Wednesday, October 4th and the final is scheduled for Wednesday,
December 13th.
Course Information
Course Information
Grades are based on
| Quizzes | 50% |
| Group Projects | 20% |
| Exams | 30% |
and the scale
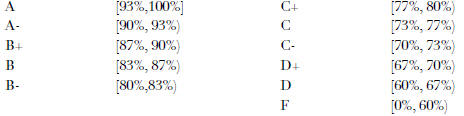
In coordination with the Disability Resource Center,
reasonable accommodations will be provided for
qualified students with disabilities. If you need accommodations because of
special exceptionalities, please
meet with Brynja Kohler during the first week of the semester to make
arrangements. Accommodations
and alternative format print materials (e.g., large print, audio, diskette or
Braille) are available through the
Disability Resource Center, located in Taggart Student Center room 104, phone
number 797-2444.
Approximate Schedule
| Week 1 | Algebra with complex numbers |
| Week 2 | Introduction to first order differential equations |
| Week 3 | Applications of first order linear equations |
| Nonlinear first order equations | |
| Week 4 | Matrix algebra, determinants, linear independence |
| Week 5 | Introduction to linear systems |
| Week 6 | Abstract vector spaces, bases and dimension |
| Week 7 | Linear systems, eigenvalues and eigenvectors |
| Week 8-9 | Fundamental solution matrices |
| Week 10-11 | Second order linear equations |
| Week 12-13 | Higher order equations |
| Week 14-15 | Laplace transforms |
|
Week 1 (4) 8/28 0.1-0.3 1.1-1.2 quiz 1 Week 2 (3) 9/4 Labor Day 1.3-1.4 quiz 2 Week 3 (4) 9/11 Group project 1 due 1.5 0.4-0.5 quiz 3 Week 4 (4) 9/18 0.6-0.9 quiz 4 Week 5 (4) 9/25 0.10-0.11 Vector spaces quiz 5 Week 6 (4) 10/2 Vector spaces 10/4 - Midterm 2.1-2.2 Week 7 (4) 10/9 2.3-2.7 quiz 6 Week 8 (3) 10/16 Group project 2 due 0 complex numbers p.178 1,2,4,7 |
3.1,3.3 10/20 - Fall Break Week 9 (4) 10/23 3.4-3.6 quiz 7 Week 10 (4) 10/30 3.7-3.10 quiz 8 Week 11 (4) 11/6 4.1-4.4 quiz 9 Week 12 (4) 11/13 4.5-4.6 3.2 quiz 10 Week 13 (1/2) 11/20 5.1-5.2 11/22-11/24 - Thanksgiving break Week 14 (4) 11/27 5.3-5.7 quiz 11 Week 15 (4) 12/4 Group project 3 due 5.8-5.10 12/8 - Last class Final 12/13 0.10.1 definitions and
fundamental 3 second-order linear equations |
| Prev | Next |