Pre-Calculus Mathematics Quiz #4 Sample Solutions
1. Give the slope-intercept equation of the line passing
through the points (1,−3) and (5, 3).
In the space below, sketch the line.
Solution: First we ascertain the line’s slope:
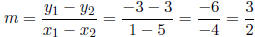
Having the line’s slope, as well as two of its points (we
now need only one of them), we can use
the point-slope equation form in order to derive the slope-intercept
equation:
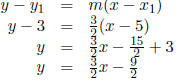 |
(point − slope form ) |
(plugging in 5, 3, and 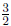 for x1, y1,m) for x1, y1,m) |
|
| ( arithmetic , algebra) | |
| (arithmetic) |
As an alternative to using the point-slope equation (as we
did above), we could have recognized
that, for some b yet to be determined, the line we seek is described by the
equation 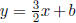 ,
,
and, in particular, this equation is satisfied by taking x and y to be x1 and
y1, respectively, for
any point (x1, y1) on the line.
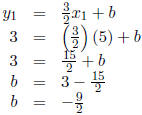 |
|
| (plugging in 5, 3 for x1, y1) | |
| (arithmetic) | |
| ( algebra ) | |
| (arithmetic) |
Having solved for b , we get that the point-slope form is
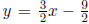 , which agrees with the
, which agrees with the
solution we obtained before. See graph in Figure 1.
2. Give the slope-intercept equation of the line that
passes through the point (−2, 3) and is
perpendicular to the line given by the equation x − 2y = 4. Sketch both lines in
the space
below.
Solution: Subtracting 4 from both sides of the given equation yields x −
2y − 4 = 0, which is
of the form Ax + By + C = 0. Recall that the slope of the corresponding line is
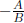 , which in
, which in
this case (with A = 1 and B = −2) is 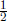 .
.
Had you not remembered this technique, you could have taken the given equation
and, by
subtracting 4 from each side , adding 2y to each side, and then dividing each
side by 2, obtained
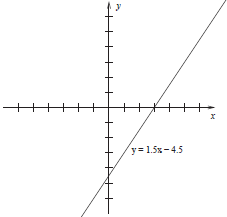
Figure 1: Answer to (1)
the equivalent equation 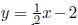 . This, of course, is
in the slope- intercept format and reveals
. This, of course, is
in the slope- intercept format and reveals
that the line has a slope of
![]() .
.
Having ascertained that ![]() is the slope of a line that is perpendicular to the line that we seek,
is the slope of a line that is perpendicular to the line that we seek,
we conclude that the line that we seek has slope −2. (After all, the product of
the slopes of
any two perpendicular lines (neither of which is vertical) is −1, and
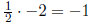 .)
.)
In addition to knowing one of its points, namely (−2, 3), now we also know the
slope of the line
that we seek, namely −2. Beginning with the point-slope equation, we derive the
slope-intercept
equation:
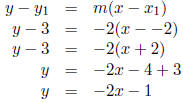 |
(point − slope form) |
| (plugging in − 2, 3,−2 for x1, y1,m) | |
| (arithmetic) | |
| (arithmetic, algebra) | |
| (arithmetic) |
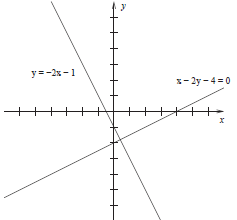
Figure 2: Answer to (2)
3. In the space below, sketch the parabola described by
the equation y = x2 + 2x + 3. Label
the vertex by its coordinates.
Solution: We use the completing-the-square method to transform the given
equation into one
of the form y = a(x − h)2 + k, which describes a parabola with vertex (h, k).
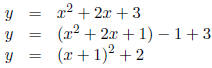 |
(given) |
| (add 1 and subtract 1) | |
| ( factoring and arithmetic ) |
We conclude that the parabola has vertex (−1, 2) and opens
upward. Indeed, the graph is just
that of y = x2 shifted one unit to the left and two units up.
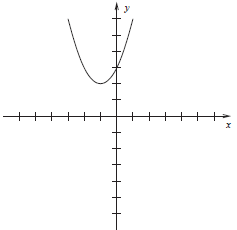
Figure 3: Answer to (3)
| Prev | Next |