Exponential and Logarithmic Functions
Composite
Functions
Section 4.1
Composite Functions
•Construct new function from two
given functions f and g
•Composite function:
•Denoted by f o g
•Read as “fcomposed with g”
•Defined by
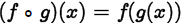
•Domain: The set of all numbers x in the
domain of g such that g(x) is in the
domain of f.
•Note that we perform the inside
function g(x) first.

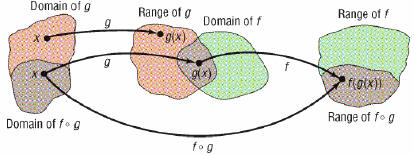
•Example. Suppose that f(x) = x3 - 2
and g(x) = 2x2+ 1. Find the values
of the following expressions .
(a) Problem: (f o g)(1)
Answer:
(b) Problem :(g o f)(1)
Answer:
(c) Problem: (f o f)(0)
Answer:
•Example. Suppose that f(x) = 2x2+ 3 and
g(x) = 4x3+ 1.
(a) Problem: Find f o g.
Answer:
(b) Problem: Find the domain of f o g.
Answer:
(c) Problem: Find g o f.
Answer:
(d) Problem: Find the domain of f o g.
Answer:
Example. Suppose that 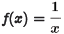 and
and
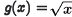
(a) Problem: Find f o g.
Answer:
(b) Problem: Find the
domain of f o g.
Answer:
(c) Problem: Find g o f.
Answer:
(d) Problem: Find the domain of
f o g.
Answer:
•Example.
Problem: If f(x) = 4x+ 2 and
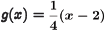 ,
show that for all x,
,
show that for all x,
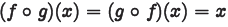
Decomposing Composite
Functions
• Example.
Problem: Find functions f and g such that
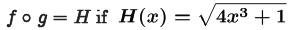
Answer:
Key Points
•Composite Functions
•Decomposing Composite Functions
One-to-One
Functions;
Inverse Functions
Section 4.2
One-to-One Functions
•One-to-one function: Any two
different inputs in the domain
correspond to two
different outputs in
the range.
•If x1 and x2 are two different inputs of a
function f, then
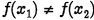
| •One-to-one
function |
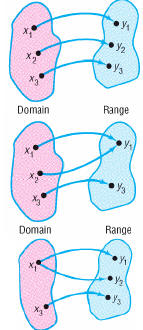 |
| •Not a one-to-one
function |
|
| •Not a function |
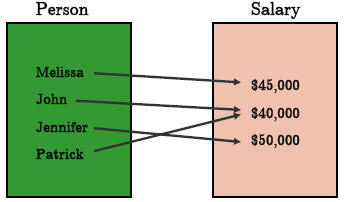
•Example.
Problem: Is this function one-to-one?
Answer:
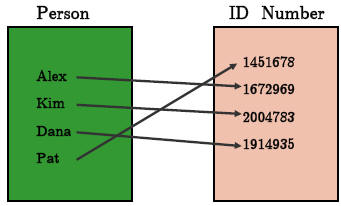
•Example. Determine whether the
following functions are
one-to-one.
(a) Problem: f(x) = x2+ 2
Answer:
(b) Problem: g(x) = x3- 5
Answer:
•Theorem.
A function that is increasing on an
interval I is a one-to-one function on
I.
A function that is decreasing on an
interval I is a one-to-one function on
I.
Horizontal- line Test
•If every horizontal line intersects the
graph of a
function fin at most one
point, then f is one-to-one.
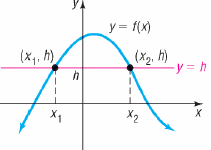
•Example.
Problem: Use the graph to determine
whether the
function is one-to-one .
Answer :
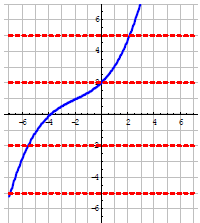
•Example.
Problem: Use the graph to determine
whether the
function is one-to-one .
Answer :
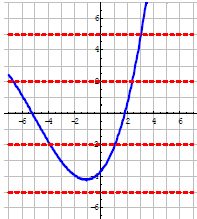
Inverse Functions
•Requires f to be a one-to-one function
•The inverse function of f
•Written f -1
•Defined as the function which takes
•f(x) as input
•Returns the output x.
•In other words, f -1undoes the action of
f
•f -1(f(x)) = x for all x in the domain of f
•f(f -1(x)) = x for all x in the domain of f -1
•Example. Find the inverse of the
function shown
Problem:
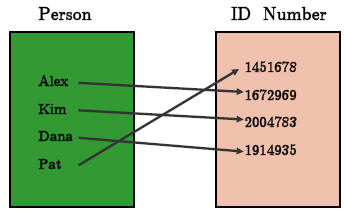
Answer:
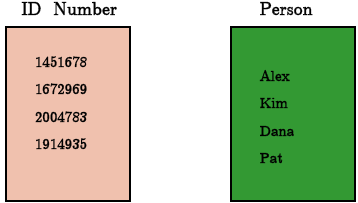
•Example.
Problem: Find the inverse of the function
shown.
{(0, 0), (1, 1), (2, 4), (3, 9), (4, 16)}
Answer:
| Prev | Next |