Ordinary Differential Equations

Objectives: MATH 365 provides an introduction to ordinary differential equations and
their applications. Upon completion of this course the student will:
• be able to solve a variety of ordinary differential equations ,
• appreciate the theory underlying the techniques of solution,
• be conversant with methods of applying ordinary differential equations in various applications.

Course Contents: Topics covered in this course may include the following.

• First order ordinary differential equations
– Linear equations with variable coefficients
– Separable equations
– Modeling with first order equations
– Autonomous equations and population dynamics
– Exact equations and integrating factors
– Existence and uniqueness theory
• Linear differential equations of second order
– Homogeneous equations with constant coefficients
– Fundamental solutions of linear homogeneous equations
– Linear independence and the Wronskian
– Complex roots of the characteristic equation
– Repeated roots ; reduction of order
– Non-homogeneous equations; method of undetermined coefficients
– Variation of parameters
– Mechanical and electrical vibrations
– Forced vibrations
• Series solutions of second order linear equations
– Series solutions near an ordinary point
– Regular singular points
– Euler equations
– Series solutions near a regular singular point
– Bessel’s equation
• The Laplace transform
– Definition of the Laplace transform
– Solution of initial value problems
– Step functions
– Differential equations with discontinuous forcing
– Impulse functions
– The convolution integral
• Systems of first order linear equations
– Review of matrices
– Systems of linear algebraic equations ; linear independence, eigenvalues, eigenvectors
– Basic theory of systems of first order linear equations
– Homogeneous linear systems with constant coefficients
– Complex eigenvalues
– Fundamental matrices
– Repeated eigenvalues

If time permits other topics may be covered as well.

Attendance: Students are expected to attend all class meetings. If you know beforehand
that you will be absent from class on the day an assignment is due, you must complete
and hand in the assignment prior to the absence. If you are unexpectedly absent the
day that an assignment is due you must hand in the assignment at the beginning of
the class hour on the first day that you return to class. If you know you will be absent
on the day of a test, you must notify me before the time the test is scheduled in order
to schedule a make-up test. Students who miss a test should provide a valid excuse,
otherwise you will not be allowed to make up the test. No final exam exemptions.

Homework: Students are expected to do their homework and participate in class. Students
should expect to spend a minimum of three hours outside of class on homework and
review for every hour spent in class. Homework exercises help students review and
reinforce concepts covered in class. The textbook exercises are arranged in generally
increasing level of difficulty. Working only the low- numbered exercises will not prepare
a student sufficiently for the test and final examination exercises. All assigned homework
exercises must be worked until successful completion. Throughout the semester
homework problems will be assigned for collection and grading. Students should submit
all homework by the date due. Late homework will not be accepted without valid
excuse. Discussion between students on homework assignments is encouraged, but
homework submitted for grading should be written up separately.

Tests: There will be three 50-minute in-class tests and a final examination. The tests are
tentatively scheduled for
• Wednesday, February 11, 2009
• Friday, March 20, 2009
• Friday, April 17, 2009

The comprehensive final examination is scheduled for Tuesday, April 28, 2009 from
10:15AM–12:15PM. I will not “ curve ” test or exam grades.

Grades: Course grade will be calculated as follows.

Tests 55%
Homework 20%
Exam 25%

Tests and the final examination will be graded individually on a 100-point scale. Homework
assignments will carry a variable number of points but will be weighted equally in
the determination of the homework grade. I keep a record of students’ test, homework,
and exam scores. Students should also keep a record of graded assignments, tests, and
other materials. As an example of the calculation of the numerical course grade, suppose
a student’s three test grades were 87, 78, and 65 (out of a maximum of 100 points
on each test), the student’s final examination grade was 71 (again, out of a maximum
of 100), and five homework assignments were collected yielding grades of 35/40, 27/50,
30/50, 25/40, and 25/35. This student’s test average is 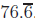. The homework grade is
calculated as

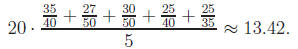
The student’s numerical course grade is then

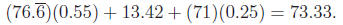
For the purposes of determining the final grade, any fraction is rounded up to the
nearest whole number.

The course letter grade will be assigned as follows. I will not “curve” course grades.

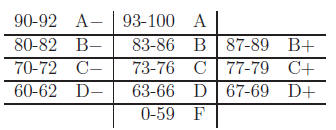
Course Repeat Policy An undergraduate student may not take an undergraduate course
of record more than three times. A course of record is defined as a course in which
a student receives a grade of A, B, C, D, (including + and −) F, U, Z or W. The
academic department offering a course may drop a student from a course if the student
attempts to take a course more than three times

Inclement Weather Policy: If we should miss a class day due to a school closing because
of weather, any activities planned for that missed day will take place the next time
the class meets. For example, if a test is scheduled for a day that class is canceled on
account of snow, the test will be given the next time the class meets.

Final Word: Mathematics is not a spectator sport. What you learn from this course and
your final grade depend mainly on the amount of work you put forth. Daily contact
with the material through homework assignments and review of notes taken during
lectures is extremely important. Organizing and conducting regular study sessions
with other students in this class will help you to understand the material better.

No one can guarantee you success in this course. Your responsibilities and the instructor’s
expectation are outlined above. There will be no second chances, “do-overs”, or
extra credit assignments.