Worksheet on Algebraic Numbers

A complex number α is called algebraic if it is the root of some polynomial
with integer coefficients, i.e. if there exists p ∈ Z[x] such that p(α) = 0. For
example:

1. 5 is algebraic because it is a root for the polynomial x - 5.

2. 1/5 is algebraic because it is a root for the polynomial 5x - 1.

3.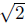is algebraic because it is a root for the polynomial x ^2 - 2.

4. i is algebraic because it is a root for the polynomial x^2 + 1, or, x^4 - 1.

Hence algebraic numbers include all integers, rationals , square roots, n-th
roots, i etc. etc. Examples of not algebraic numbers (also called transcendental)
include e and π. (it is kind of funny that even though "most numbers" are
transcendental we can only give a name to two of them ...)

Cool Theorem 1. Algebraic numbers form a field (denoted

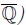
Since algebraic numbers are naturally a subset of complex numbers , we really
must check that they form a sub field of C. This means:

•the sum of two algebraic numbers is still an algebraic number.
•the product of two algebraic numbers is still an algebraic number.
•the multiplicative inverse of an algebraic number is still an algebraic number.

I can almost feel the buzz in the back of your heads going "DUH!" - but think
about it for a second! This is really not at all obvious!!! We have seen above
the polynomials that do the job for 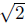and i. Can you tell me a polynomial
(with integer coefficients!!) for which 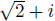is a root?

The goal of this worksheet is to get an intuition for how this theorem works
and how to construct the polynomials that kill sums and products of algebraic
numbers! And at that point it will still take some theory and hard work to
eventually PROVE the theorem!!

Problem 1. Let's warm up first. For each of the numbers below, find a polynomial with integer coefficients that kills it, and write down the other roots of such a polynomial:

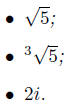
Problem 2. Consider the number 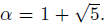Can you find a polynomial p
with integer coefficients such that p(α) = 0?

Let us try to look for a quadratic polynomial - here we know (or we should
remember) the quadratic formula , and we can reverse engineer the answer... and
now observe: what is the other root of this polynomial? Also, can you relate
the degree of the polynomial p to the degrees of the polynomials annhilating 1
and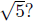

Problem 3. Let us now look for a polynomial with integer coefficients for which
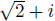is a root. Let us again make a wild guess and *hope* we can find a
polynomial of degree 4 that does the job. Take the generic polynomial of the
form:

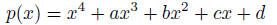
Plug in x = 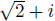and try to solve the system of linear equations in a, b, c, d
coming from setting to 0 the coefficients of 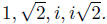Now that you have
found the polynomial, factor it and look at the other roots!

(There is really an interesting linear algebra story here - those four numbers
can be considered as Q-linearly independent vectors and therefore the only way
that a linear combination of them gives 0 is by each coefficient being 0, but
that's a subtler story we don't need to be concerned with at the moment...)

Let us keep in mind our goal: relating the roots of the polynomial that kills
α + β to the roots of the polynomials killing α and β individually. Any ideas?

Problem 4. Make a conjecture on how to construct the polynomial killing α + β
knowing the polynomials that kill α and β . Once you have a conjecture, test it
on some more examples! Does it work?

If you don't have a conjecture yet, try constructing by hand some other example. For example, can you find a degree 3 polynomial that kills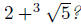

Now you have a conjecture for how to show that the sum of two algebraic
numbers is still algebraic.

Problem 5. Can you do the same work for a product of algebraic numbers?
I.e. can you tell me a conjecture for how to construct a polynomial with integer
coefficients that kills αβ starting from the polynomials that kill α and β? Test
your conjecture and make sure it works.

Hopefully you have now a good intuition of how this theorem works and
\why" it is true. If you have any remaining time, start thinking if you can
devise any strategy to prove this fact in general. Remember, so far we only
have a philosphy - not a proof! And that's what we are after!