Vertex Form
In the previous section , you learned that it is a simple
task to sketch the graph of a
quadratic function if it is presented in vertex form
f(x) = a(x − h)2 + k. (1)
The goal of the current section is to start with the most
general form of the quadratic
function, namely
f(x) = ax2 + bx + c, (2)
and manipulate the equation into vertex form. Once you
have your quadratic function
in vertex form, the technique of the previous section should allow you to
construct the
graph of the quadratic function.
However, before we turn our attention to the task of
converting the general quadratic
into vertex form, we need to review the necessary algebraic fundamentals. Let’s
begin
with a review of an important algebraic shortcut called squaring a binomial.
Squaring a Binomial
A monomial is a single algebraic term, usually constructed
as a product of a number
(called a coefficient) and one or more variables raised to nonnegative integral
powers,
such as −3x2 or 14y3z5. The key phrase here is “single term.” A binomial is
an algebraic
sum or difference of two monomials (or terms), such as x + 2y or 3ab2 − 2c3.
The key
phrase here is “ two terms .”
To “square a binomial,” start with an arbitrary binomial,
such as a+b, then multiply
it by itself to produce its square (a + b)(a + b), or, more compactly, (a +
b)2. We can
use the distributive property to expand the square of the binomial a + b.
(a + b)2
= (a + b)(a + b)
= a(a + b) + b(a + b)
= a2 + ab + ba + b2
Because ab = ba, we can add the two middle terms to arrive at the following property.
Property 3. The square of the binomial a + b is expanded as follows.
(a + b)2 = a2 + 2ab + b2 (4)
 Example 5. Expand (x + 4)2.
Example 5. Expand (x + 4)2.
We could proceed as follows.
(x + 4)2
= (x + 4)(x + 4)
= x(x + 4) + 4(x + 4)
= x2 + 4x + 4x + 16
= x2 + 8x + 16
Although correct, this technique will not help us with our
upcoming task. What
we need to do is follow the algorithm suggested by Property 3.
as follows:
1. Square the first term to get a2.
2. Multiply the first and second terms together, and then multiply the result by
two to get 2ab.
3. Square the second term to get b2.
Thus, to expand (x + 4)2, we should proceed as follows.
1. Square the first term to get x2
2. Multiply the first and second terms together and then multiply by two to get
8x.
3. Square the second term to get 16.
Proceeding in this manner allows us to perform the
expansion mentally and simply
write down the solution.
(x + 4)2 = x2 + 2(x)(4) + 42 = x2 + 8x + 16
Here are a few more examples. In each, we’ve written an
extra step to help clarify
the procedure. In practice, you should simply write down the solution without
any
intermediate steps.
(x + 3)2 = x2 + 2(x)(3) + 32 = x2 + 6x + 9
(x − 5)2 = x2 + 2(x)(−5) + (−5)2 = x2 − 10x + 25
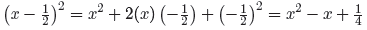
It is imperative that you master this shortcut before
moving on to the rest of the
material in this section.
Perfect Square Trinomials
Once you’ve mastered squaring a binomial, as in
(a + b)2 = a2 + 2ab + b2, (6)
it’s a simple matter to identify and factor trinomials
(three terms) having the form
a2 + 2ab + b2. You simply “undo” the multiplication. Whenever you spot a
trinomial
whose first and third terms are perfect squares, you should suspect that it
factors as
follows.
a2 + 2ab + b2 = (a + b)2 (7)
A trinomial that factors according to this rule or pattern
is called a perfect square
trinomial.
For example, the first and last terms of the following trinomial are perfect squares.
x2 + 16x + 64
The square roots of the first and last terms are x and 8,
respectively. Hence, it makes
sense to try the following.
x2 + 16x + 64 = (x + 8)2
It is important that you check your result using
multiplication. So, following the
three-step algorithm for squaring a binomial:
1. Square x to get x2.
2. Multiply x and 8 to get 8x, then multiply this result by 2 to get 16x.
3. Square 8 to get 64.
Hence, x2 + 16x + 64 is a perfect square trinomial and factors as (x + 8)2.
As another example, consider x2 − 10x + 25. The square
roots of the first and last
terms are x and 5, respectively. Hence, it makes sense to try
x2 − 10x + 25 = (x − 5)2.
Again, you should check this result. Note especially that
twice the product of x and
−5 equals the middle term on the left, namely, −10x.
Completing the Square
If a quadratic function is given in vertex form, it is a
simple matter to sketch the
parabola represented by the equation. For example, consider the quadratic
function
f(x) = (x + 2)2 + 3,
which is in vertex form. The graph of this equation is a
parabola that opens upward.
It is translated 2 units to the left and 3 units upward. This is the advantage
of vertex
form. The transformations required to draw the graph of the function are easy to
spot
when the equation is written in vertex form.
It’s a simple matter to transform the equation f(x) = (x +
2)2 + 3 into the general
form of a quadratic function, f(x) = ax2 + bx + c. We simply use the three-step
algorithm to square the binomial; then we combine like terms .
f(x) = (x + 2)2 + 3
f(x) = x2 + 4x + 4 + 3
f(x) = x2 + 4x + 7
Note, however, that the result of this manipulation, f(x)
= x2+4x+7, is not as useful
as vertex form, as it is difficult to identify the transformations required to
draw the
parabola represented by the equation f(x) = x2 + 4x + 7.
It’s really the reverse of the manipulation above that is
needed. If we are presented
with an equation in the form f(x) = ax2 +bx+c, such as f(x) = x2 +4x+7, then
an
algebraic method is needed to convert this equation to vertex form f(x) = a(x−h)2+k;
or in this case, back to its original vertex form f(x) = (x + 2)2 + 3.
The procedure we seek is called completing the square. The
name is derived from
the fact that we need to “complete” the trinomial on the right side of y = x2 +
4x + 7
so that it becomes a perfect square trinomial.
square involves three key steps.
1. Take half of the coefficient of x and square the
result.
2. Add and subtract the quantity from step one so that the right-hand side of
the
equation does not change.
3. Factor the resulting perfect square trinomial and combine constant terms.
Let’s follow this procedure and place f(x) = x2 + 4x + 7 in vertex form.
1. Take half of the coefficient of x. Thus, (1/2)(4) = 2.
Square this result. Thus,
22 = 4.
2. Add and subtract 4 on the right side of the equation f(x) = x2 + 4x + 7.
f(x) = x2 + 4x + 4 − 4 + 7
3. Group the first three terms on the right-hand side.
These form a perfect square
trinomial.
f(x) = (x2 + 4x + 4) − 4 + 7
Now factor the perfect square trinomial and combine the
constants at the end to
get
f(x) = (x + 2)2 + 3.
That’s it, we’re done! We’ve returned the general
quadratic f(x) = x2 + 4x + 7
back to vertex form f(x) = (x + 2)2 + 3.
Let’s try that once more.
| Prev | Next |