Systems of First Order Linear Equations Part 2
• If a real matrix A has a complex eigenvalue
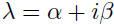then
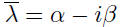must also be an eigenvalue.
• This follows from the fact that det(A − λI) is a
polynomial of
degree n with real coefficients.
• We want real valued solutions to
x′ = Ax
• The eigenvectors of A corresponding to λ and
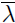will be complex .
Eigenvectors of Conjugate Eigenvalues
Lemma 21.1. If the matrix
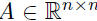has conjugate eigenvalues
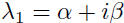and
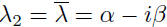with eigenvectors
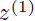and
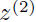
respectively then
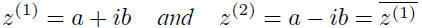
where a ∈ Rn and b ∈ Rn
Proof. This follows from direct computation. Since for any two complex
scalars we know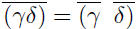 
we have
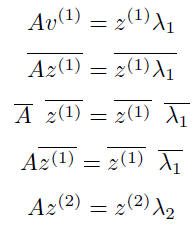
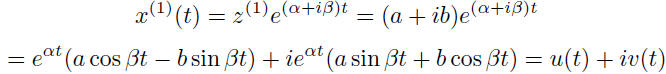
If can be shown that u(t) and v(t) are linearly independent solutions to
the ODE.
If the matrix A ∈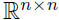 
has conjugate eigenvalues
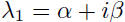and
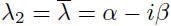with eigenvectors
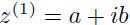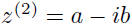and 
and
distinct eigenvalues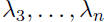 
with real eigenvectors
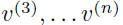then a
general solution of x ′ = Ax is
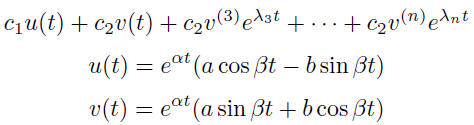
The result is straightforward to adapt to multiple conjugate pairs and
distinct real eigenvalues .
Example
Textbook p. 401
x′ = Ax
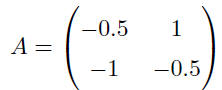
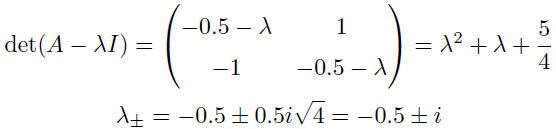
Example
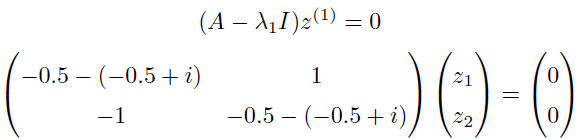z1
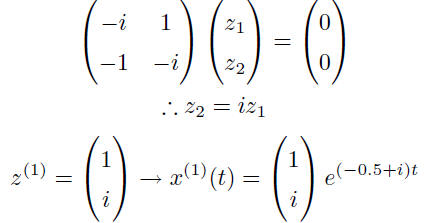
Example
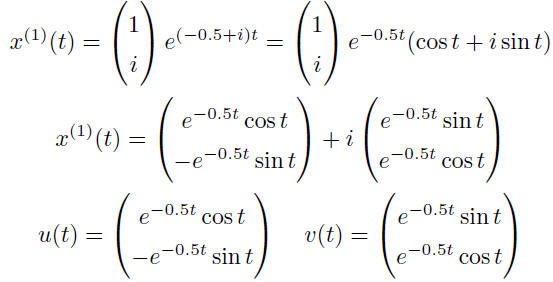
Example
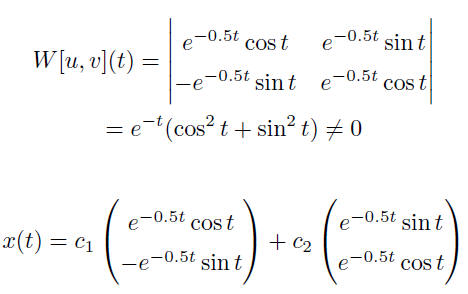
| Prev | Next |