Solving Inequalities

An inequality is similar to an equation except that the statement is that two expressions have a
relationship other than equality, such as <, ≤, >, or ≥.

To solve an inequality means to find all values of the variable that make the inequality true.

Rules for Inequalities

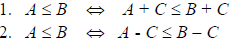
3. If C > 0, then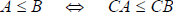
4. If C < 0, then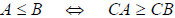
5. If A > 0 and B > 0, then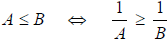
6. If A ≤ B and C ≤ D, then A + C ≤ B + D

Linear Inequalities

A linear inequality is one in which each term is constant or a multiple of the variable.

Nonlinear Inequalities

The Sign of a Product or Quotient
If a product or quotient has an even number of negative factors, then its value is positive.
If a product or quotient has an odd number of negative factors , then its value is negative .

To Solve a Nonlinear Inequality:
1. Write the inequality so that all nonzero terms are on side of the inequality sign. If there
are fractions , write the expression with a single fraction.
2. Factor the nonzero side of the inequality.
3. Determine the values for which each factor is zero and divide the number line into the
intervals.
4. Use test values to make a diagram using the number line, showing the sign of each factor
on each interval.
5. Determine the solution from the table of signs. Check the endpoints of the intervals with
the inequality.

Example 1: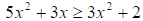

Example 2: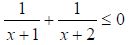

Absolute Value Inequalities

Properties of Absolute Value Inequalities

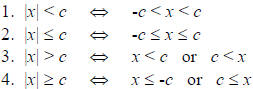
Example 3: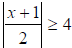

Example 4: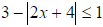

Applications Involving Inequalities

Example 5: Jenny has 120 feet of fencing. She wants to enclose a rectangular pen for her
chickens, and she wants the area enclosed to be at least 800 square feet . What range of values is
possible for the length of her pen?

Example 6: The average height of adult males is 68.2 inches, and 95% of adult males have
height h within 5.8 inches of that height. Write an absolute value inequality that expresses the
relationship.

Example 7: In the vicinity of a bonfire, the temperature T in °C at a distance of x meters from
the center of the fire was given by 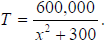  At what range of distances from the fire’s
center was the temperature less than 500°C?